Лингвистические и семиотические представления
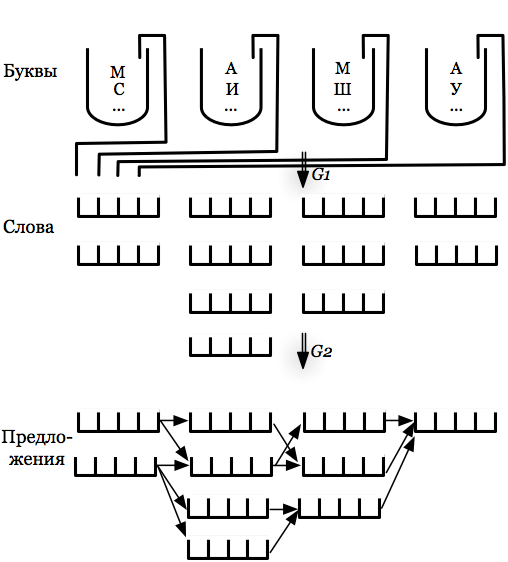
Рис. 2.11
Математическая лингвистика и семиотика — самые «молодые» методы формализованного отображения систем. Включение их в разряд математических нельзя считать общепризнанным.
Математическая лингвистика возникла во второй половине XX в. как средство формализованного изучения естественных языков и вначале развивалась как алгебраическая лингвистика.
Основными понятиями, на которых базируются лингвистические представления, являются понятия: тезаурус, грамматика, семантика, прагматика.
Термин тезаурус (от греч. θησαυρός, thesаurоs — сокровищница, богатство, клад, запас и т.п.) в общем случае характеризует совокупность научных знаний о явлениях и законах внешнего мира и духовной деятельности людей, накопленную всем человеческим обществом.
В математической лингвистике и семиотике термин «тезаурус» используется в более узком смысле, для характеристики конкретного языка, его многоуровневой структуры. Для этих целей удобно пользоваться одним из принятых в лингвистике определений тезауруса как «множества смысловыражающих элементов языка с заданными смысловыми отношениями».
Это определение позволяет представить структуру языка в виде уровней (страт) множеств (например, слов, словосочетаний, предложений, абзацев и т.п.), смысловыражающие элементы каждого из которых формируются из элементов предшествующих структурных уровней (рис. 2.11).
Правила (G1, G2) формирования смысловыражающих элементов второго и третьего уровней в тезаурус не входят, в тезаурусе определяется только вид и наименование уровня, характер и вид смысловыражающих элементов.
Под грамматикой (которую иногда называют синтактикой, синтаксисом, что сужает понятие грамматики, исключая из него морфологию) понимаются правила, с помощью которых формируются смысловыражающие элементы языка (на рис. 2.11 приведены два вида правил — G1 и G2, которые иногда называют грамматиками 1-го и 2-го рода). Пользуясь правилами, можно «порождать» (формировать) грамматически (синтаксически) правильные конструкции или распознавать их грамматическую правильность.
Термин «грамматика» употребляется в лингвистике и как укороченная замена термина «формальная грамматика».
Под семантикой понимается содержание, значение, смысл формируемых или распознаваемых конструкций языка; под прагматикой — полезность для данной цели, задачи.
В естественном языке различить понятия, с помощью которых характеризуются термины «семантика» и «прагматика», трудно.
Поэтому принято рассматривать эти понятия на примерах. Поясним различие между семантически и прагматически правильными конструкциями языка на следующих легко запоминающихся примерах.
Предложение «Муха лукаво всплеснула зубами» синтаксически правильное, но не имеет смысла в естественном русском языке в обиходном, широком употреблении, т.е. является с точки зрения пользователей русским языком семантически неправильным (исключим пока гипотетическую ситуацию сказки, в которой муха может быть наделена указанными свойствами).
Другое предложение «Маленькая девочка собирает цветы на лугу» синтаксически и семантически правильное. Однако для директора завода (если это луг, а не заводской газон, и — учтем личный фактор — если эта девочка не его дочь) это предложение не несет никакой информации, т.е. прагматически (с точки зрения целей руководителя) является неправильным. Другое дело, если «Иванов (который в данный момент должен находиться на рабочем месте) собирает цветы на лугу». Тогда это предложение было бы и прагматически правильным.
Возвратимся теперь к примеру с мухой. Приведенное предложение, семантически неправильное, может в гипотетической ситуации сказки оказаться прагматически правильным что важно иметь в виду при применении лингвистических представлений.
При создании и использовании искусственных языков применяют такие понятия структурной лингвистики, как порождающая и распознающая грамматика.
Под порождающей грамматикой понимается совокупность правил, с помощью которых обеспечивается возможность формирования (порождения) из первичных элементов (словаря) синтаксически правильных конструкций. Под распознающей грамматикой — правила, с помощью которых обеспечивается возможность распознавания синтаксической правильности предложений, фраз или других фрагментов языка.
Все рассмотренные понятия в равной мере используются как в математической лингвистике, так и в лингвистической семиотике. Некоторую условную границу между ними можно провести, лишь введя понятие «классы формальных грамматик» (как теорий математической лингвистики).
Формальный язык определяется как множество (конечное или бесконечное) предложений (или «цепочек»), каждое из которых имеет конечную длину и построено с помощью некоторых операций (правил) из конечного множества элементов (символов), составляющих алфавит языка. Формальную грамматику определяют в виде четверки множеств: $$G=<V_T,V_N,R,A>,$$
где %%V_T%% — множество основных (терминальных) символов; %%V_N%% — множество вспомогательных (нетерминальных) символов; %%R%% — множество правил вывода, или продукций, которые могут иметь вид $$\alpha \rightarrow \beta.$$
(здесь %%\beta \in (V \cup V_N)%% т.е. %%\beta%% — цепочка конечной длины из терминальных и нетерминальных символов множеств %%V_T%% и %%V_N%%; $$\alpha \in (V_T\cup V_N)V_N(V_T\cup V_N),$$
т.е. %%\alpha%% является цепочкой из терминальных и нетерминальных символов, содержащей по крайней мере один нетерминальный символ из %%V_N%%); %%A%% — множество аксиом (%%A%% состоит из одного начального символа %%S%%, причем %%S\subset V_N%%).
Семиотика возникла как наука о знаках, знаковых системах. Однако некоторые школы, развивающие семиотические представления, настолько равноправно пользуются в семиотике понятиями математической лингвистики, такими, как тезаурус, грамматика, семантика и т.п., не выделяя при этом в отдельное направление лингвосемиотику, что часто трудно определить, к какой области относится модель — математической лингвистике или семиотике.
В то же время именно в лингвосемиотике достигнуты наиболее конструктивные результаты, которые могут быть полезны при исследовании систем различной физической природы.
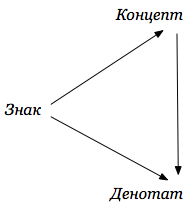
Рис. 2.12
Семиотические представления пользуются другими по сравнению с математической лингвистикой средствами исследования семантических возможностей языков. В частности, используют понятия «знак», «знаковая ситуация». Треугольник Г. Фреге (рис. 2.12), согласно которому любой знак имеет форму (десигнат, собственно знак), денотат (означаемое знака) и концепт (смысл, значение). Треугольник Фреге характеризует отношения знака, денотата и концепта. Концепт позволяет определить денотат в соответствующем аспекте, в конкретной знаковой ситуации.
В нашей стране лингвосемиотику развивал Ю. А. Шрейдер, который
- ввел понятие «знаковая ситуация» как пары из знака и обозначаемого (означаемого) данным знаком;
- сформулировал основные особенности знака: 1) способность знака в ряде случаев замещать обозначаемое; 2) нетождественность знака и денотата (знак никогда не может полностью заменить означаемое); 3) многозначность соответствия «знак-денотат» (конвенциональность обозначений);
- интерпретировал концепт как информацию, которую знак несет о возможных денотатах, об их положении в системе реалий, месте в универсуме;
- показал, что выбор денотата зависит от конкретной ситуации, сориентироваться в которой помогает концепт;
- ввел понятие знаковой системы как набора знаков, в котором есть какие-то внутренние отношения между обозначаемыми;
- установил соответствия: знак — семантика, текст — смысл, сообщение — информация и показал, что текст может выполнять двойную функцию — знака и сообщения.
В частности, на границе лингвистики и семиотики возникли языки синтагматического типа, т.е. языки, использующие правила типа %%\{a_i r_k b_j\}%%, называемые синтагмой, где %%a_i\in A; b_j\in B%% — взаимодействующие множества (подклассы) исходных понятий языка; %%r_k\in R%% — множество отношений, которые могут иметь произвольный вид. Однако такая свобода приводит к увеличению числа антиномий в языке.
Поэтому используемые отношения конкретизируют. В частности, Ю. А. Шрейдер исследовал возможности использования отношений эквивалентности, толерантности и строгого порядка, определяемых на основе свойств рефлексивноcти, симметричности и транзитивности (табл. 2.7).
Таблица 2.7
| Отношение | Рефлексивноcть | Симметричность | Транзитивность |
|---|---|---|---|
| Эквивалентность | + | + | + |
| Толерантность | + | + | - |
| Строгий порядок | - | - | + |
Для пояснения возможностей, появляющихся при таком подходе к созданию языка, проиллюстрируем применение отношения толерантности. Как очевидно из табл. 2.7, по определению толерантность — особый вид сходства, при котором сопоставляемые элементы языка находятся в отношении, обладающем рефлексивностью и симметричностью, но не обладающем транзитивностью. Это означает, что, например, если при сопоставлении слов ввести допустимую ошибку в один символ, то отношение сходства между первым и вторым словами могут быть признаны (с точностью до допустимой ошибки) рефлексивным и симметричным; аналогично — между вторым и третьим; но первое и третье слова уже могут отличаться не одним, а двумя символами, и сходство между ними можно вообще не обнаружить, т.е. не будет выполнено отношение транзитивности.
Возникновение подобных ситуаций важно учитывать при разработке языков для формального кодирования передачи текстов и восстановления их в месте приема.
С помощью отношения толерантности можно отобразить некоторые отношения между словами естественного языка. Например,
| рам-а %%\tau%% стол |
| стол %%\tau%% книг-у, |
где %%\tau%% — операция установления сходства. Приведенные соотношения означают, что в синтагме «рама %%\tau%% стол» имеет место отношение сходства с точностью до рефлексии и симметрии, в синтагме «стол %%\tau%% книгу» — тоже, а между элементами синтагмы «рам-а» — «книг-у» сходства нет в силу невыполнения по определению для рассматриваемого отношения свойства транзитивности.
Попытаемся интерпретировать формальную запись. Содержательный анализ этих соотношений позволяет понять, что в них отражено сходство по падежу. Слова мужского рода («стол») могуг употребляться в русском языке в одинаковой форме в именительном (первая строка) и винительном (вторая строка) падеже, в то время, как слова женского рода имеют в этих падежах разную форму, что и обусловило нетранзитивность.
Таким образом, вводя в язык отношение толерантности (например, путем формирования классов толерантности) можно отразить в языке взаимоотношения между словами и высказываниями более полно и точно, чем это позволяют делать отношения математической логики. Такие языки необходимы при расшифровке древних рукописей, при автоматизации процесса перевода с одного языка на другой.
| Математическая логика | Графические методы |