Графические методы

В рассматриваемой классификации к классу графических представлений отнесены такие средства отображения результатов анализа информации, как графики, диаграммы, гистограммы, древовидные структуры, которые можно отнести к средствам активизации интуиции специалистов, графики Ганта, (т.е. «время-операция» в прямоугольных координатах и т.д.) и возникшие на основе графических отображений теории: теория графов, теория сетевого планирования и управления и т.п., т.е. все, что позволяет наглядно представить процессы, происходящие в системах, и облегчить таким образом их анализ для человека (лица, принимающего решения).

Классификация применяемых графиков по признакам и видам приведена в табл. 2.8.

Таблица 2.8

Группы по признакам	Виды
1. Графики, выражающие структуры и связи (оргаграммы)	Классификационные схемы. Схемы организационных структур. Оргасхемы табличного и другого типов. Схемы прохождения информации в документах. Схемы рабочих процессов (оперограммы)
2. Графики, выражающие расположения предметов и явлений во времени (хронограммы) и в пространстве (топограммы)	Контрольно-планировочные графики. Гармонограммы и т.п. Маршрутные графики. Планы расположения предметов и рабочих мест и т.п.
3. Графики, выражающие количественные отношения	Графики сравнения величин (простые и групповые). Гистограммы. Графики, выражающие структурные сравнения. Графики изменения и распределения величин
4. Графики расчетного характера	Номограммы. Шкалограммы и т.п.

Есть и возникшие на основе графических представлений методы, которые позволяют ставить и решать вопросы оптимизации процессов организации, управления, проектирования, и являются математическими методами в традиционном смысле.

Таковы геометрия, теория графов.

Исторически понятие «графа» первоначально было введено Л. Эйлером.

Основные понятия теории графов приведены в табл. 2.9, которая поможет начать самостоятельное ее изучение.

Таблица 2.9

Понятие	Определение (определяющий признак)	Изображение
Граф (Г)	Множества элементов %%x_0, x_1, ..., x_n%% и отношений %%r_0, r_1, ..., r_m%% между ними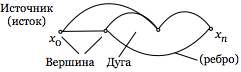
Граф конечный по x	Конечное множество элементов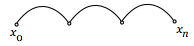
Граф конечный по r	Конечное множество отношений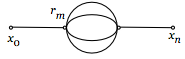
Граф ненаправленный (неориентированный)	Элементы неупорядочены. Направление отношений не определено
Граф направленный (ориентированный)	Элементы упорядочены. Направление отношений определено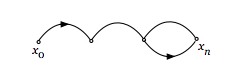
Граф симметрический	Двусторонние отношения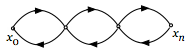
Граф асимметрический	Односторонние отношения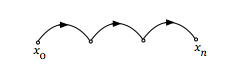
Граф несвязный	Обособленные части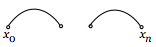
Граф сильно связный	Любые два элемента соединены хотя бы одним путем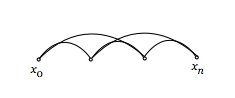
Граф полный	Любая пара элементов соединена непосредственно хотя бы одним отношением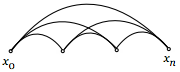
Мультиграф	Много отношений между некоторыми элементами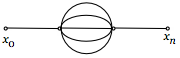
Цикл (для ребер). Контур (для дуг)	Замкнутые последовательности элементов и отношений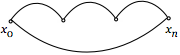
Петля	Контур единичной длины, связывающий точку x саму с собой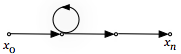
Цепь (для ребер). Путь (для дуг)	Последовательность элементов и отношений
Прадерево	Один источник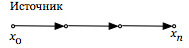
Дерево	Не менее двух вершин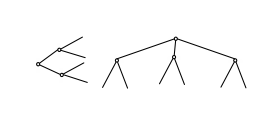
Сеть. Сетевой график	Соединение элементов, удовлетворяющее требованиям, предъявляемым к направленным графам (наличие источника, стока и отсутствие циклов)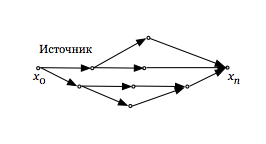
Структура системы	Любое соединение элементов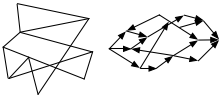

Графические представления позволяют наглядно отображать структуры сложных систем и процессов, происходящих в них. С этой точки зрения их можно рассматривать как промежуточные между МФПС и МАИС.

Особую роль в моделировании процессов в сложных системах проектирования и управления играют представления операций во времени. Старейшими из таких представлений являются графики Ганта («время-операция» в прямоугольных координатах), которые первоначально применялись при планировании, контроле и управлении производством.

Графики Ганта выполнялись в форме чертежей, ленточных диаграмм с ручным, а в последующем и с автоматическим управлением. В последнем случае графики представляли собой бесконечные ленты, одна половина которых была окрашена в черный цвет (черный участок соответствовал продолжительности операции).

Дальнейшим шагом было разделение лент на отрезки времени, отображающие дискретные операции, что позволяло оперировать с дискретной информацией. В последующем на этой основе возникли представления совокупности дискретных операций в дискретном времени как множества событий, упорядоченных в двух измерениях — сетевые структуры. Далее на этой основе возникли прикладные теории — PERT (методика оценки и контроля программ), сетевого планирования и управления, а позднее и ряд методов статистического сетевого моделирования с использованием вероятностных оценок графов.

Первоначально методы СПУ широко применялись не только в управлении производственными процессами (где достаточно несложно построить сетевой график), но и в системах организационного управления.

Однако в последнем случае важно понимать основные недостатки СПУ.

Во-первых, эта теория первоначально была ориентирована на анализ только одного класса графов — направленных (не имеющих обратных связей, т.е. циклов, петель; такие требования содержались в руководящих материалах по формированию сетевых планов предприятий), и это явилось одной из причин того, что впоследствии при применении сетевых методов для отображения ситуаций, не подчиняющихся этим ограничениям, был использован термин «сетевое моделирование», снимающий требование о том, чтобы граф имел только одно направление.

Во-вторых, (что наиболее существенно) при формировании сетевых планов необходимо участие высококвалифицированных специалистов, хорошо знающих процессы в системе (эту работу нельзя поручить техническим работникам, которые полезны лишь при оформлении сетевых графиков и обработке результатов оценки).

Для снижения доли «ручного» труда полезно сочетать графические представления с лингвистическими и семиотическими, разрабатывая языки автоматизации формирования сетевой модели. На основе такого сочетания методов возникли новые направления моделирования — стрyкmурно-лингвистическое, графо-семиотическое и т.п.