Математическая логика
Базовыми понятиями математической логики являются высказывание, предикат, логические функции (операции) кванторы, логический базис, логические законы (законы алгебры логики).
Под высказыванием в алгебре логики понимается повествовательное предложение (суждение), которое характеризуется определенным значением истинности.
В простейших случаях используется два значения истинности: «истинно» — «ложно», «да» — «нет», «1» — «0». Такая алгебра логики, в которой переменная может принимать только два значения истинности, называется бинарной алгеброй логики Буля (по имени ее создателя).
Предикат — выражение, грамматически имеющее форму высказывания, но содержащее переменные некоторых подмножеств, на которых они определены.
Применение переменных высказываний служит для выражения общности и позволяет формулировать законы алгебры логики для любых высказываний данного вида.
Из одного или нескольких высказываний (предикатов) можно образовать новые высказывания (предикаты). Объединение простых высказываний в сложные производится без учета смысла этих высказываний (предикатов) на основе определенных логических правил (операций, функций).
Число простейших логических функций в конкретной алгебре логики зависит от количества значений истинности n: $$N=2^{2^n}.$$
Для двузначной булевой алгебры логики %%N%% определяется числом возможных двоичных наборов (%%n%%=2): %%N%% = 16. При %%n%% = 3 можно образовать %%N%% = 256 логических функций. Функции бинарной алгебры логики приведены в табл. 2.4, в которой собраны формы записи и наименования функций, встречающиеся в различных учебниках и монографиях по математической логике.
Таблица 2.4
| Способы алгебраической записи логических функций | Основные названия логической функции (оператора, фактора) | Двоичная система записи | Условные названия |
|---|---|---|---|
| %%F_1=0%% | Тождественный нуль. Тождественно ложно | 0000 | Любое можно |
| %%F_2=1%% | Тождественная единица. Тождественно истинно | 1111 | Любое истинно |
| %%F_3=a%% | Утверждение первого аргумента (переменного воздействия). Повторение первого аргумента. Доминация первого переменного | 1100 | Как %%a%% |
| %%F_4=b%% | Утверждение второго аргумента (переменного воздействия). Повторение второго аргумента (переменного). Доминация второго переменного | 1010 | Как %%b%% |
| %%F_5=a\cup b%% %%A\lor b, a\div b%% | Дизъюнкция. Логическая сумма. Объединение. Простая (неразделительная) дизъюнкция. Сборка. Абстрагирование. Комбинация. Автономия. Констелляция | 1110 | И/или Или, хотя бы |
| %%F_6=a\cap b; a\land b%% %%a%% & %%b;%% %%a\cdot b; a\times b%% | Конъюнкция. Логическое произведение. Перечисление. Совпадение. Соединенное суждение. Частное утвердительное суждение | 1000 | И И И |
| %%F_7=a\equiv b; a\sim b;%% %%a\leftrightarrow b; a=b%% | Эквивалентность. Равнозначность. Материальная эквивалентность. Взаимность. Солидарность. Комплементарность. Интердепенденция | 1001 | Как |
| %%F_8=a\supset b;%% %%a\to b; a>b%% | Импликация. Следование. Материальная импликация. Общеутвердительное суждение. Селекция. Спецификация. Детерминация. Обратная антиимпликация | 1011 | Если то Только |
| %%F_9=ab;%% %%a\cup b; a\lor b%% | Функция Вэбба. Операция Пирса. Отрицание дизъюнкции. Обратная дизъюнкция. Антидизъюнкция. Обратная логическая сумма. Гетерофазис. Недизъюнкция. Отрицание комбинации, автономии и т.д. Антиконстелляция | 0001 | Не или Ни ни |
| %%F_{10}=a/b; a\cap b%% %%a\land b; a\cdot b; a\times b;%% %%a%% & %%b%% | Функция Шеффера. Операция Шеффера. Штрих Шеффера. Отрицание конъюнкции. Обратная конъюнкция. Неконъюнкция. Обратное логическое произведение. Обратное совпадение. Альтернативное отрицание. Несовместимость. Общеотрицательное суждение | 0111 | Не и Или не |
| %%F_{11}=a\neq b; a\equiv b;%% %%a\oplus b;%% %%a%% w %%b%% | Отрицание равнозначности. Функция разноименности. Функция сложения по модулю. Неравнозначность. Строгая дизъюнкция. Исключающая дизъюнкция. Разделительная дизъюнкция. Отрицание взаимозависимости | 0110 | Не как Или или |
| %%F_{12}=a<b;%% %%a\subset b; a\gets b%% | Обратная импликация. Обратное следование. Обратная селекция. Обратная спецификация. Обратная детерминация | 1101 | Или не |
| %%F_{13}=\neg a;a\sim a;%% %%a^c;ca%% | Отрицание первого аргумента. Инвертация первого аргумента (переменного). Дополнение к первому переменному. Профазис | 0011 | Не %%a%% |
| %%F_{14}=\overline b; \neg b; b';%% %%\sim b; b^c cb%% | Отрицание второго аргумента. Инвертация второго аргумента (переменного). Дополнение ко второму переменному. Обратный антифазис | 0101 | Не %%b%% |
| %%\overline \supset%% %%F_{15}=a\backslash b;%% %%A^{\not \supset}%% %%b; a%% %%b; a\rightarrow b%% | Отрицание материальной импликации. Материальная антиимпликация. Антисовпадение. Разделительное суждение. Отрицание селекции. Антиселекция. Антиспецификация. Антидетерминация | 0100 | Но не |
| %%\overline \subset%% %%F_{16}=a\not \subset \overline b;%% %%A%% %%b;%% %%a\leftarrow b%% | Отрицание обратной импликации. Обратная антиимпликация. Обратное разделительное суждение. Обратное антисовпадение | 0010 | Не но |
Кроме логических функций, в логике предикатов имеются еще операции квантификации — кванторы. Это специальные операции, которые служат для выражения общности суждений и связанных с ними понятий (табл. 2.5) и позволяют на формальном языке исчисления предикатов говорить не об одном объекте, а о целом классе объектов.
Таблица 2.5
| Обозначения | Названия | Смысл |
|---|---|---|
| %%(\forall%% %%a)%% %%b%% | Квантор общности | Для любого %%a%% будет %%b%% |
| %%(\exists%% %%a)%% %%b%% | Квантор существования | Есть хотя бы одно %%a%% такое, что будет %%b%% |
| %%(%% E! %%a)%% %%b%% | Квантор единственности | Есть только одно %%a%% такое, что будет %%b%% |
В этой связи существуют понятия дизъюнктивной нормальной и конъюнктивной нормальной формы, всегда удовлетворяющие требованиям базиса.
В условиях выполнения требований к базису в алгебре логики доказывают теоремы, демонстрирующие свойства операций над высказываниями. Применяя эти теоремы, формально можно получить правильный результат, не вникая в смысл проводимых исследований. Примеры этих теорем (логических законов) приведены в табл. 2.6.
Таблица 2.6
| Название свойства (закона), формулировки | Символическая запись |
|---|---|
| Замкнутость Множество %%R%% содержит дизъюнкцию и конъюнкцию всех входящих в него элементов | %%a\cup b\in R%% %%a\cap b\in R%% |
| Коммутативность Изменение последовательности элементов не изменяет значения дизъюнкции и конъюнкции | %%a\cup b=b\cup a%% %%a\cap b=b\cap a%% |
| Ассоциативность Группировка внутри конъюнкции и дизъюнкции не меняет их значений | %%(a\cap b)\cap c=a\cap (b\cap c)%% %%(a\cup b)\cup c=a\cup (b\cup c)%% |
| Дистрибутивность Прибавление элемента к произведению равносильно прибавлению этого элемента к сомножителям; умножение суммы на элемент равносильно умножению слагаемых на этот элемент | %%a\cup (b\cap c)=(a\cup b)\cap (a\cup c)%% %%a\cap (b\cup c)=(a\cap b)\cup (a\cap c)%% |
| Идемпотентность (закон технологии) Повторение элемента (прибавление или умножение) не изменяет истинности элемента | %%a\cup a=a%% %%a\cap a=a%% |
| Совместимость | %%a\cup b=b%% в том и только том случае, если %%a\cap b=b%% |
| Дополнительность Для каждого элемента %%a%% множества %%R%% существует дополнение %%\neg a%% или %%R-a%% | Частный случай %%a\cup \neg a=R,%% %%\neg R=\varnothing%% %%a\cap \neg a=\varnothing,%% %%\neg\varnothing=R%% |
| Законы поглощения (абсорбции) Дизъюнкция произведения и одного из ее членов эквивалентна этому члену. Конъюнкция суммы и одного из ее членов эквивалентна этому члену | %%a\cup (a\cap b)\equiv a%% %%a\cap (a\cup b)\equiv a%% |
| Законы двойственности (теоремы А. де Моргана) Дополнение к пересечению %%a%% и %%b%% эквивалентно объединению их дополнений. Дополнение к объединению элементов (множеств) равно пересечению их дополнений | %%\overline {a\cap b}\equiv \overline {a}\cup \overline b%% %%\overline {a\cup b}\equiv \overline a\cap \overline b%% |
| Инволюция (закон удвоенного отрицания) | %%\neg (\neg a) \equiv \overline a%% |
| Законы противоположности Если элемент %%a%% эквивалентен дополнению элемента %%b%%, то элемент %%b%% эквивалентен дополнению элемента %%a%% | %%a \equiv \overline b \Rightarrow b \equiv \overline a%% |
| Множество содержит элементы %%R=1%% и %%\varnothing=0%% такие, что для всякого элемента | %%a\cup \varnothing = a, a\cup R=R%% %%a \cap R=R, a\cap \varnothing=a%% |
| Умножение одного из элементов на дополнение второго элемента не меняет дизъюнкции элементов | %%a \cdot (\neg b) \equiv a+b%% %%a \cap (\neg b) \equiv a\cup b%% |
Полную систему логических функций называют логическим базисом. Чтобы система функций представляла собой базис, она должна обладать определенными свойствами.
В частности, чтобы система функций была полной, необходимо и достаточно, чтобы она содержала хотя бы одну функцию: не сохраняющую константу «единица», не сохраняющую константу «нуль», нелинейную, немонотонную, несамодвойственную.
Полный логический базис содержит избыточное число функций. Такая система функции может остаться базисом при удалении из нее некоторых функций. Удаление функций можно производить до тех пор, пока система не станет такой, что удаление из нее хотя бы одной из функций, ее образующих, будет приводить к невыполнению перечисленных требований к базису. Такую систему называют минимальным базисом.
Минимальными базисами бинарной алгебры логики являются базисы, включающие только две функции %%\{\neg, \cup\} \{\neg, \cap\}%%. Функция отрицания не сохраняет константы «нуль» и «единицу» и не является монотонной, функции дизъюнкции %%\cup%% и конъюнкции %%\cap%% обеспечивают нелинейность и не являются самодвойственными.
Из элементарных функций алгебры логики формируют последовательности действий, отображающие процессы в системе от входа до выхода, т.е. логические алгоритмы.
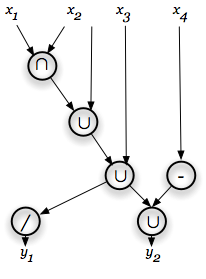
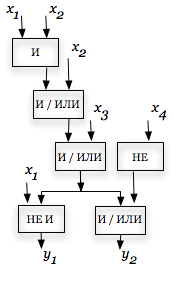
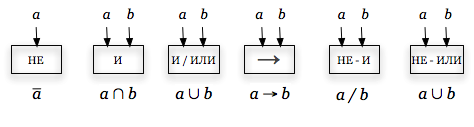
На рис. 2.7 и 2.8 проиллюстрирована разная запись одного и того же алгоритма (соответствие обозначений рис. 2.7 и 2.8 приведено на рис. 2.9).
 |  |
|---|---|
| Рис. 2.7 | Рис. 2.8 |
 |
|---|
| Рис. 2.9 |
Этот же алгоритм может быть записан следующим образом:
$$y_1=x_1/ \{[(x_1\cap x_2)\cup x_2]\cup x_3\};$$
$$y_2=x_4\cup \{[(x_1\cap x_2)\cup x_2]\cup x_3\}.$$
Существует много форм записи логических алгоритмов: в виде функций алгебры логики, в форме таблиц или матриц, «машин Тьюринга», логических схем по А. А. Ляпунову, с помощью рекурсивных функций, на языке нормальных алгоритмов А. А. Маркова, ввиде программ для вычислительных машин на одном из языков программирования, в форме диаграмм Насси — Шнайдермана.
Логические алгоритмы можно преобразовывать с использованием логических законов. Пример применения одного из законов (теоремы А. де Моргана) приведен на рис. 2.10.
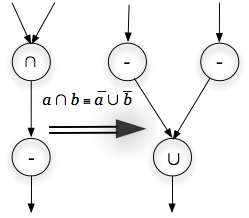
Рис. 2.10
На базе логических представлений возникли и развиваются теории логического анализа и логического синтеза. Эти теории основаны на применении средств алгебры логики к задачам анализа и синтеза структур исследуемых систем, а также к задачам принятия решений в сложных проблемных ситуациях, возникающих в системах или при взаимодействии систем.
Задача логического анализа состоит в описании поведения системы с известной структурой набором системно-логических уравнений (функций алгебры логики — ФАЛ) и исследования полученного логического выражения с целью его минимизации (осуществляется путем применения законов алгебры логики, приведенных в табл. 2.6), т.е. выяснения, нельзя ли получить более простую структуру (схему), содержащую меньшее число элементов (состояний), но осуществляющую требуемые преобразования. Такие задачи возникают, например, при создании автоматических систем контроля неисправностей, систем автоматического резервирования, обеспечения надежности и т.д.
| Теоретико-множественные представления | Лингвистические и семиотические представления |