2.1. Проблема принятия решения
Поскольку необходимость в методах моделирования возникает при решении каких-либо конкретных задач, то для выбора классификации методов вначале рассмотрим проблему принятия решения.
В тех случаях, когда решение задачи базируется на законах физики, химии и других фундаментальных областей знаний или когда задача может быть поставлена в терминах конкретного класса прикладных задач, для которого разработан соответствующий математический аппарат, применять термин «проблема принятия решения» нет необходимости. Потребность в этом термине возникает в тех случаях, когда задача настолько усложняется, что для ее постановки и решения не может быть сразу определен подходящий аппарат формализации, когда процесс постановки задачи требует участия специалистов различных областей знаний. Это приводит к тому, что постановка задачи становится проблемой, для решения которой нужно разрабатывать специальные подходы, приемы, методы. В таких случаях возникает необходимость определить область проблемы принятия решения (проблемную ситуацию); выявить факторы, влияющие на ее решение; подобрать приемы и методы, которые позволят сформулировать или поставить задачу таким образом, чтобы решение было принято.
Поясним процесс принятия решения на упрощенном примере — задаче по перемещению из одного пункта в другой. Такого рода задачи возникают при доставке грузов на предприятие, выпускаемой продукции — потребителю, и наконец, — повседневно перед каждым человеком при поездке из дома на работу.
Пример
В терминах «проблемы принятия решения» эту задачу можно представить следующим образом (рис. 2.1).
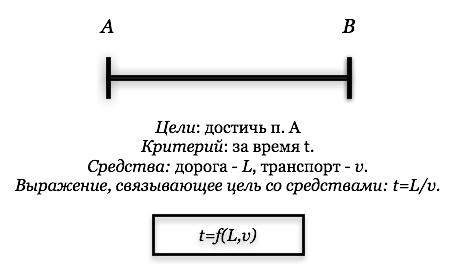 |
|---|
| Рис. 2.1 |
Дано: цель — достичь пункта %%A%% (или переместить груз из пункта %%B%% в пункт %%A%%) и возможные средства — путь (дорога) и транспорт (различные транспортные средства передвижения или средства доставки грузов).
Требуется: обеспечить реализацию цели.
Если нет никаких других оговорок, требований, то задачи нет, поскольку безразлично, какой маршрут и какие транспортные средства выбирать. Для того чтобы возникла необходимость принимать решение (возникла задача), нужно ввести критерий (или несколько критериев), отражающий требования к достижению цели. Аналогично нет задачи и в тех случаях, когда ЛПР не может задать требования, сформулировать критерий достижения цели или неизвестен набор средств достижения цели, т.е. имеет место задача с неопределенностью. В качестве критерия в рассматриваемой задаче можно, например, принять требование осуществить перемещение «за время %%t%%» или «к такому-то времени %%t%%».
Для решения задачи нужно определить взаимосвязи цели со средствами ее достижения, что в данной задаче легко сделать путем оценки средств (дорога оценивается длиной пути %%L%%, транспорт — скоростью %%v%% транспортного средства; в простейшем случае — средней скоростью) и установления связей этих оценок с критерием. В данном случае в качестве выражения, связывающего цель со средствами, можно использовать закон движения, который в случае равномерного прямолинейного движения имеет вид %%t = L/v%%, а в общем виде %%t = f(L, v)%%.
Таким образом, для принятия решения нужно получить выражение, связывающее цель со средствами ее достижения с помощью вводимых критериев оценки достижимости цели и оценки средств (см. рис. 2.1).
Такие выражения получили в параллельно возникавших прикладных направлениях различные названия: критерий функционирования; критерий, или показатель, эффективности; целевая, или критериальная, функция; функция цели и т.п.
При постановке рассматриваемой задачи могут быть учтены не только обязательные, основные требования, отражаемые с помощью критерия, но и дополнительные требования, которые могут выступать в качестве ограничений (в данной задаче это могут быть затраты на создание или приобретение средства транспортировки грузов, наличие денежных средств у человека, выбирающего вид транспорта и т.п.).
Тогда для решения задачи формируют комплекс соотношений, включающий наряду с основным выражением, связывающим цель со средствами, соотношения-неравенства, к правило, неравенства (хотя в принципе могут быть и равенствами). Разработан широкий спектр методов решения задач математического программирования. Его важные принципиальные особенности будут кратко охарактеризованы ниже.
Выражения, связывающие цель со средствами ее достижения, могут представлять собой не только простые соотношения, подобные рассмотренным выше, но и более сложные, составные критерии (показатели) аддитивного или мультипликативного вида. Конечно в этом случае могут возникнуть вычислительные сложности, при преодолении которых может потребоваться вновь обратиться к постановке задачи. Однако полученное формализованное ее представление позволяет в дальнейшем применять и формализованные методы анализа проблемной ситуации.
В то же время при постановке задачи в числе критериев могут быть и принципиально неформализуемые. Например, даже в рассмотренной, простейшей задаче наряду с критерием времени и ограничением по затратам можно учесть и такие, принципиально неформализуемые критерии, как безопасность транспортировки грузов для рабочих, удобство приведения в действие транспортно-распределительных устройств или их остановки, а также такой критерий, который определяется термином «комфорт».
Пример
С учетом последнего критерия, даже при коротких расстояниях и небольшом выигрыше во времени, можно выбрать такси вместо общественного транспорта, если конечно позволяют денежные средства; или при передвижении между населенными пунктами иногда лучше выбрать более длинную, но асфальтированную дорогу, чем более короткую, но ухабистую.
Можно выбирать транспортное средство с учетом вида груза. Например, в случае скоропортящейся продукции лучше использовать более дорогостоящий рефрижератор, чем обычный грузовой автомобиль и т.д.
В рассмотренных выше случаях полностью формализованная постановка задачи оказывается нереализуемой. Возможны и другие реальные ситуации, затрудняющие формализацию критериев или формирование выражения, связывающего цель со средствами.
Получить такие выражения легко, если известен закон, позволяющий связать цель со средствами (в рассмотренном примере — закон движения). Если закон неизвестен, то стараются определить закономерности на основе статистических исследований либо исходя из наиболее часто встречающихся на практике экономических или функциональных зависимостей. Если и это не удается сделать, то выбирают или разрабатывают теорию, в которой содержится ряд утверждений и правил, позволяющих сформулировать концепцию и сконструировать на ее основе процесс принятия решения. Если и теории не существует, то выдвигается гипотеза, и на ее основе создаются модели, с помощью которых исследуются возможные варианты решения.
В общем виде для ситуаций различной сложности процесс отображения проблемной ситуации можно представить, воспользовавшись многоуровневыми структурами типа «слоев» М. Месаровича (рис. 2.2).
При постановке конкретной задачи могут присутствовать не все уровни, приведенные на рис. 2.2.
Пример
Далеко не всегда существует теория. Два верхних уровня можно менять местами, т.е. начинать исследование с выбора теории или формулирования концепции, а затем на их основе формировать модель.
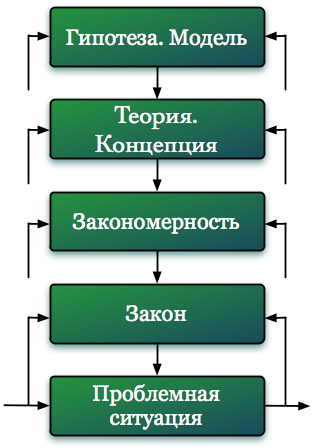 |
|---|
| Рис. 2.2 |
По поводу термина «модель» существуют разные точки зрения. Первоначально потребность в применении этого термина возникла, когда не удавалось решить задачу строго математическими методами, но в последующем формализованные остановки типа рассмотренной, также стали называть моделями.
Наиболее краткое и точное определение модели дал С. Лем: «Моделирование — это подражание природе, учитывающее немногие ее свойства». При этом он поясняет, что «немногие» не из-за неумения, а для защиты от избытка информации. Модель учитывает важные для цели исследования факторы и отсевает малозначимые.
В этом смысле можно говорить о механических, математических, компьютерных и т.п. моделях. Любая из них может рассматриваться как отображение реального объекта или процесса, которое учитывает свойства, интересующие исследователя.
При решении задач организации современного производства необходимо учитывать все большее число факторов различной природы, являющихся предметом исследования различных областей знаний. В этих условиях один человек не может принять решение о выборе факторов, влияющих на достижение цели, не может определить существенные взаимосвязи между целями и средствами; в формировании и анализ ее модели принятия решения должны участвовать коллективы разработчиков, состоящие из специалистов различных областей знаний, между которыми нужно организовать взаимодействие и взаимопонимание; а проблема принятия решений становится проблемой выбора целей, критериев, средств и вариантов достижения цели, т.е. проблемой коллективного принятия решения.
Число и сложность подобных проблем, для которых невозможно сразу получить критерий эффективности в аналитической форме, по мере развития цивилизации возрастает; возрастает также и цена неверно принятого решения. Для проблем принятия решения характерно, как правило, сочетание качественных и количественных методов. Принятие решений в системах управления промышленностью часто связано с дефицитом времени: лучше принять не самое хорошее решение, но в требуемый срок, так как в противном случае лучшее решение может уже и не понадобиться. Поэтому решение часто приходится принимать в условиях неполной информации (ее неопределенности или даже дефицита), и нужно обеспечить возможность как можно в более сжатые сроки определить наиболее значимые для принятия решений сведения и наиболее объективные предпочтения, лежащие в основе принятия решения.
Чтобы помочь в более сжатые сроки поставить задачу, проанализировать цели, определить возможные средства, отобрать требуемую информацию (характеризующую условия принятия решения и влияющую на выбор критериев и ограничений), а в идеале — получить выражение, связывающее цель со средствами, применяют системные представления, приемы и методы системного анализа.
| Глава 2. Методы и модели теории систем и системного анализа | 2.2. Подходы к анализу и проектированию систем |