Статистические методы

Статистические методы. Статистические представления сформировались как самостоятельное научное направление в середине прошлого века (хотя возникли значительно раньше). Основу их составляет отображение явлений и процессов с помощью случайных (стохастических) событий и их поведений, которые описываются соответствующими вероятностными (статистическими) характеристиками и статистическими закономерностями.

Термин «стохастические» уточняет понятие «случайный», которое в обыденном смысле принято связывать с отсутствием причин появления событий.

Статистические отображения системы в общем случае (по аналогии с аналитическими) представлены символическим образом, как бы в виде «размытой» точки (размытой области) в n-мерном пространстве, в которую переводит учитываемые в модели свойства системы оператор Ф %%[S_x]%%. Границы области заданы с некоторой вероятностью р («размыты») и движение точки описывается некоторой случайной функцией.

Напомним, что под вероятностью события понимается %%p(A)= m/n%% (где %%m%% — число появлений события %%A%%; %%n%% — общее число опытов), если при %%n → \infty (m/n) → const%%.

Закрепляя все параметры этой области, кроме одного, получим «срез» по линии а—b, смысл которого — воздействие данного параметра на поведение системы, которое можно описать статистическим распределением по этому параметру, одномерной статистической закономерностью. Аналогично можно получить двумерную, трехмерную и т.д. картины статистического распределения.

Статистические закономерности можно представить в виде дискретных случайных величин и их вероятностей или в виде непрерывных зависимостей распределения событий, процессов.

Для дискретных событий соотношение между возможными значениями случайной величины %%x_i%% и их вероятностями %%p_i%% называют законом распределения и либо записывают в виде ряда (табл. 2.2), либо представляют в виде зависимостей %%F(x)%% (рис. 2.5, а) или %%p(x)%% (рис. 2.5, в).

Таблица 2.2

%%x%%	%%x_1%%	%%x_2%%	...	%%x_i%%	...	%%x_n%%
%%p(x)%%	%%p_1%%	%%p_2%%	...	%%p_i%%	...	%%p_n%%

---

При этом $$F(x)=\sum_{x_i<x}p_i(x_i).$$

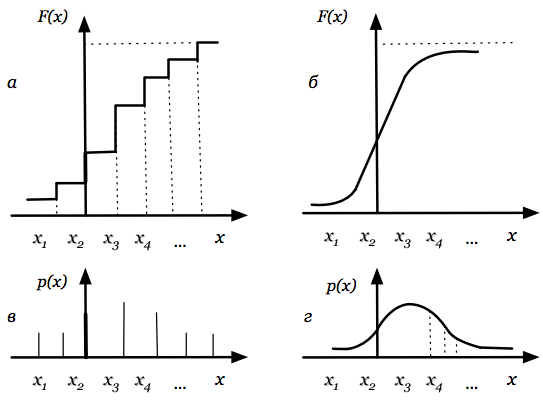
Рис. 2.5

Для непрерывных случайных величин (процессов) закон распределения представляют (соответственно дискретным законам) либо в виде функции распределения (интегральный закон распределения — рис. 2.5, б), либо в виде плотности вероятностей (дифференциальный закон распределения — рис. 2.5, г). в этом случае

%%p(x)=dF(x)/dx%%     и    %%\Delta F(x)=p(x)\Delta x,%%

где %%p(x)%% — вероятность попадания случайных событий в интервал от %%x%% до %%x + \Delta x%%

Закон распределения является удобной формой статистического отображения системы.

Однако получение закона (даже одномерного) или определение изменений этого закона при прохождении через какие-либо устройства или среды представляет собой трудную, часто невыполнимую задачу. Поэтому в ряде случаев пользуются не распределением, а его характеристиками — начальными и центральными моментами.

Наибольшее применение получили:

• 1-й начальный момент — математическое ожидание или среднее значение случайной величины:

  %%m_x=\sum\limits_{i=1}^nx_ip_i(x_i)%%— для дискретных величин;

  %%m_x=\int\limits_{-\infty}^{\infty}p(x)dx%%— для непрерывных величин;

• 2-й центральный момент — дисперсия случайной величины:

  %%\sigma_x^2=\sum\limits_{i=1}^n(x_i-m_x)^2p_i(x_i)%%— для дискретных величин;

  %%\sigma_x^2=\int\limits_{-\infty}^\infty(x-m_x)^2p(x)dx%%—для непрерывных величин.

Для полной группы несовместных событий имеют место условия нормирования:

• для функции распределения

$$\sum_{i-1}^n p_i(x_i)=1;$$

• для плотности вероятности

$$\int\limits_{-\infty}^{\infty}p(x)dx=F(\infty)-F(-\infty)=1-0=1.$$

На практике иногда используется не дисперсия %%\sigma_x^2%%, а среднее квадратическое отклонение %%\sigma_x%%.

Связь между случайными величинами в общем случае характеризуется ковариацией — моментом связи; для двумерного распределения ковариация обозначается %%cov(x, y)%%, или %%m_{xy}%%, или %%M[(x-m_x)(y-m_y)]%%.

Использование ковариации в качестве меры связи случайных переменных не всегда удобно, так как величина ковариации зависит от единиц измерения, в которых измерены случайные величины. При переходе к другим единицам измерения ковариация тоже изменяется, хотя степень связи случайных переменных, естественно, остается прежней. Поэтому в качестве меры связи признаков нередко используют ковариацию нормированных отклонений — коэффициент корреляции

$$r=cov(x',y')-M\Bigg[\frac{(x-m_x)(y-m_y)}{\sigma_x\sigma_y}\Bigg]M,$$

где %%x'=(x-m_x)/\sigma_x, y'=(y-m_y)/\sigma_y%% — нормированные отклонения; %%\sigma_x%%, %%\sigma_y%% — среднеквадратические отклонения.

Коэффициент корреляции может представляться и другими способами.

Практическое применение получили в основном одномерные распределения, что связано со сложностью получения статистических закономерностей и доказательства адекватности их применения для конкретных приложений, которое базируется на понятии выборки.

Под выборкой понимается часть изучаемой совокупности явлений, на основе исследования которой получают статистические закономерности, присущие всей совокупности и распространяемые на нее с какой-то вероятностью.

Для того чтобы полученные при исследовании выборки закономерности можно было распространить на всю совокупность, выборка должна быть представительной (репрезентативной), т.е. обладать определенными качественными и количественными характеристиками. Качественные характеристики связаны с содержательным аспектом выборки, т.е. с определением, являются ли элементы, входящие в нее, элементами исследуемой совокупности, правильно ли отобраны эти элементы с точки зрения цели исследования (с этой точки зрения выборка может быть случайной, направленной или смешанной).

На базе статистических представлений развивается ряд математических теорий, которые можно разделить на четыре основные группы:

• математическая статистика, объединяющая различные методы статистического анализа (регрессионный, дисперсионный, корреляционный, факторный и т.п.);
• теория статистических испытаний;

основой этой теории является метод Монте-Карло; развитием — теория статистического имитационного моделирования;

• теория выдвижения и проверки статистических гипотез;

возникла для оценки процессов передачи сигналов на расстоянии; базируется на общей теории статистических решающих функций;

• теория потенциальной помехоустойчивости;

обобщает последние два направления теории статистических решений.

Перечисленные направления в большинстве своем носят теоретико-прикладной характер и возникали из потребностей практики. На их основе развивается ряд прикладных научных направлений: экономическая статистика, теория массового обслуживания, статистическая радиотехника, статистическая теория распознавания образов, стохастическое программирование, новые разделы теории игр и т.п.

Расширение возможностей отображения сложных систем и процессов по сравнению с аналитическими методами можно объяснить тем, что применение статистических представлений процесс постановки задачи как бы частично заменяется статистическими исследованиями, позволяющими, не выявляя все детерминированные связи между изучаемыми объектами (событиями) или учитываемыми компонентами сложной системы, на основе выборочного исследования (исследования репрезентативной выборки) получать статистические закономерности и распространять их на поведение системы в целом.

В то же время не всегда может быть определена репрезентативная выборка, доказана правомерность применения полученных на ее основе статистических закономерностей. Если не удается доказать репрезентативность выборки или для этого требуется недопyстимо большое время, то применение статистических методов может привести к неверным результатам. В таких случаях целесообразно обратиться к методам, объединяемым под общим названием — методы дискретной математики, которые помогают разрабатывать языки моделирования, модели и методики постепенной формализации процесса принятия решения.