Метод Парето решения многокритериальных задач выбора альтернативы
Предположим, что необходимо решить задачу выбора альтернативы из множества возможных по двум критериям W1 и W2, которые требуется максимизировать. Множество X состоит из конечного числа n возможных решений %%x_1%%, %%x_2%%, ..., %%x_n%%. Каждому решению соответствует определенные значения показателей W1 и W2 (рис. 15). Множество решений представлено на плоскости с координатами W1 W2.
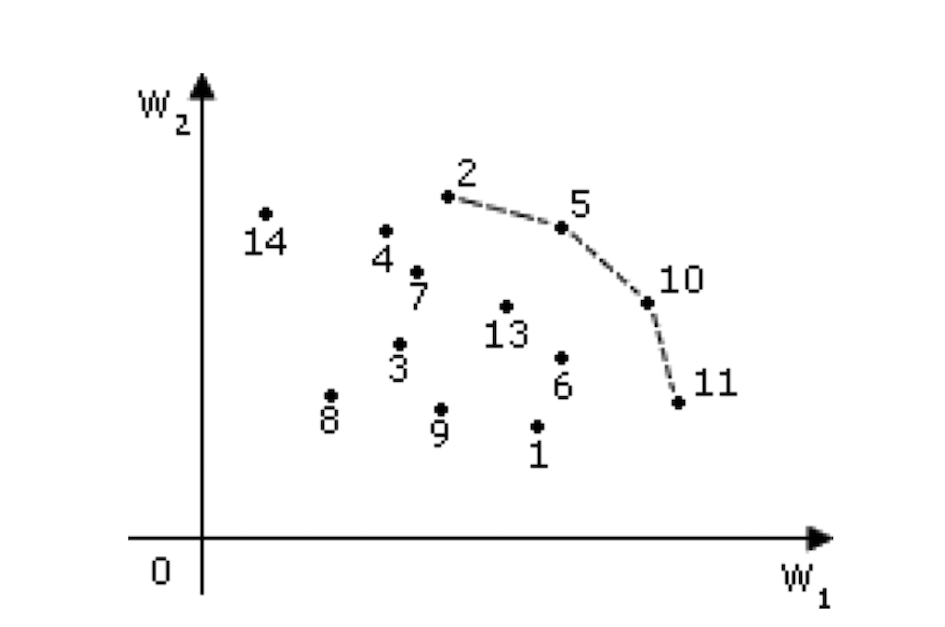
Рисунок 15. Метод Парето
Очевидно, что из всего множества X эффективными будут только решения %%x_2%%, %%x_5%%,%%x_{10}%%, %%x_{11}%%, лежащие на правой верхней границе области возможных решений. Для всякого другого решения существует хотя бы одно доминирующее решение, для которого либо W1, либо W2, либо оба больше, чем для данного. И только для решений, лежащих на правой верхней границе, доминирующих решений не существует.
Когда из множества возможных решений выделены эффективные, дальнейший выбор можно вести уже в пределах этого «эффективного» множества, что радикально упрощает решение задачи. На рис. 15 эффективное множество образуют четыре решения: %%x_2%%, %%x_5%%,%%x_{10}%%, %%x_{11}%%, из которых %%x_{11}%% – наилучшее по критерию W1, а %%x_2%% – по критерию W2. Лицо, принимающее решение, должно теперь выбрать вариант, который для него предпочтителен по обоим критериям.
| Нахождение решений в условиях определенности при множественности целей | Парадоксы интуитивных предпочтений |