Принятие решений в условиях неопределенности
Нигда сам не принимай решения, если ты сможешь сделать так, чтобы его принял кто- либо другой.
Принцип Пфайфера
Принятие решения в условиях неопределенности имеет место, когда то или иное действие (или все действия) приводит к множеству возможных исходов, вероятности которых ЛПР неизвестны.
Нередко результат решения зависит от наступления определенных внешних ситуаций, которые не только не контролируются ЛПР, но и по которым у него отсутствует информация, при какой из этих ситуаций его решение должно быть эффективным. Особая трудность появляется, когда при конкретных внешних ситуациях каждый раз оптимальной была бы другая альтернатива. Выбор решения в таких условиях и называют принятием решения в условиях неопределенности.
Рассмотрим пример.
Пример
Таблица 21. Матрица решений
| А1 | 92 | 160 | 40 | Р1 | Р2 | Р3 | |
| А2 | 100 | 76 | 120 | А1 | 92 | 160 | 40 |
| А3 | 68 | 80 | 140 | А2 | 100 | 76 | 120 |
| А4 | 62 | 74 | 105 | А3 | 68 | 80 | 140 |
Левая половина — исходная матрица, правая — после исключения неэффективной альтернативы
Целью является увеличение прибыли фирмы либо за счет нового продукта (альтернатива А1), либо за счет завоевания нового рынка (А2), либо за счет кооперации с другими фирмами (А3), либо за счет увеличения активности на существующих рынках (А4). Все четыре альтернативы приводят к разным результатам в зависимости от возможной конъюнктуры и условий конкуренции (Р1, Р2, Р3).
Для начала может быть выполнен предварительный отбор альтернатив на основе принципов принятия решений. В частности, альтернатива А4 может быть исключена, т.к. она не эффективна по сравнению с альтернативой А3.
Для выбора альтернативы в условиях неопределенности разработан ряд стратегий:
- правило Вальда (максимин-правило), иногда носит название минимакс-правило; его можно было бы назвать также правилом монашки: «береженого Бог бережет»;
- максимакс-правило, называемое иногда минимин-правилом; его можно характеризовать русской поговоркой «кто не рискует, тот не пьет шампанское»;
- правило Гурвича, называемое иногда правилом оптимизма- пессимизма; его можно характеризовать русской поговоркой «Бог не выдаст, свинья не съест»;
- правило Сэвиджа–Нигана, называемое иногда правилом минимакса сожаления;
- правило Лапласа;
- правило Крелле.
Правило Вальда ориентируется на ЛПР, настроенное пессимистично и стремящееся минимизировать потери. Оно признает только минимальную прибыль, но не убытки и выбирает опцию, которая максимизирует минимальную прибыль.
Для каждой внешней ситуации фиксируется минимальное значение, а потом из этих худших значений выбирается максимальное (табл. 22).
Пример (продолжение)
Наиболее приемлемой альтернативой при этом подходе альтернатива А2.
Таблица 22. Правило Вальда
| Р1 | Р2 | Р3 | Правило минимакса | |
| А1 | 92 | 160 | 40 | 40 |
| А2 | 100 | 76 | 120 | 76 |
| А3 | 68 | 80 | 140 | 68 |
 Максимакс-правило ориентируется на предельно оптимистичное ЛПР, для которого определяющим является только результат, достигаемый в лучшем случае.
Пример (продолжение)
В нашем примере выбирается альтернатива А1 (табл. 23).
Таблица 23. Правило максимакса
| Р1 | Р2 | Р3 | Правило максимакса | |
| А1 | 92 | 160 | 40 | 160 |
| А2 | 100 | 76 | 120 | 120 |
| А3 | 68 | 80 | 140 | 140 |
 Правило Гурвича представляет собой компромисс между двумя рассмотренными стратегиями. При этом для каждой альтернативы учитываются два значения – максимальное и минимальное. Для этого вводится дополнительный параметр оптимизма-пессимизма α, который учитывает индивидуальный подход ЛПР к риску. У пессимиста α лежит в диапазоне от 0 до 0,5, у оптимиста – от 0,5 до 1.
Далее каждый максимум в строчке умножается на α, а каждый минимум – на (1−α). Для случая умеренного пессимиста (α = 0,3) результат представлен в табл.24.
Пример (продолжение)
Таблица 24. Правило Гурвича (правило оптимизма-пессимизма)
| Р1 | Р2 | Р3 | Правило Гурвича | |
| А1 | 92 | 160 | 40 | 160х0,3 + 40х0,7 = 76 |
| А2 | 100 | 76 | 120 | 120х0,3 + 76х0,7 = 89,2 |
| А3 | 68 | 80 | 140 | 140х0,3 + 68х0,7 = 89,6 |
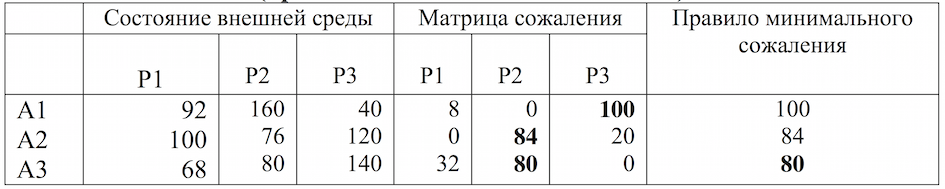
В стратегии Сэвиджа–Нигана ЛПР ориентируется не на абсолютный результат, а на минимизацию максимально плохого результата. Для этого вычисляется таблица «сожалений». В ней для каждого состояния внешней среды, по каждой альтернативе вычисляется убыток/ущерб, который получается при выборе данной альтернативы по сравнению с оптимальной альтернативой (табл. 25). Для каждой альтернативы отмечаем максимальный ущерб. Выбираем альтернативу с минимумом максимального ущерба.
Достоинство этого подхода заключается в том, что минимизируется максимально возможная ошибка. Это отражает позицию пессимистичного или по крайней мере осторожного ЛПР.
Пример (продолжение)
Таблица 25. Правило Сэвиджа-Нигано (правило минимального сожаления)
Правило Лапласа предполагает, что ЛПР имеет нейтральное отношение к риску. Оно позволяет выбрать альтернативу с максимальной суммарной пользой. Для этого каждому состоянию внешней среды приписывается равная вероятность (которая определяется как 1, деленная на число рассматриваемых состояний среды). Далее определяется сумма для каждой альтернативы.
Пример (продолжение)
Оптимальной для нашего примера оказывается альтернатива А2.
Таблица 26. Правило Лапласа
| Р1 | Р2 | Р3 | Правило Лапласа | |
| А1 | 92 | 160 | 40 | 92х0,33 + 160х0,33 + 40х0,33 = 97,33 |
| А2 | 100 | 76 | 120 | 100х0,33 + 76х0,33 + 120х0,33 = 98,67 |
| А3 | 68 | 80 | 140 | 68х0,33 + 80х0,33 + 140х0,33 = 96 |
С помощью правила Крелле пытаются учесть индивидуальные предпочтения ЛПР в отношении риска. Для этого необходимо определить индивидуальную функцию предпочтений ЛПР, что представляет собой сложную задачу. Затем все значения для каждой альтернативы пересчитываются с помощью этой функции в цифры полезности в глазах ЛПР. Если бы удалось достаточно объективно определить эту функцию субъективных предпочтений ЛПР, правило Крелле могло бы быть весьма эффективным. Но поскольку возможность ее надежного определения остается спорной, правило Крелле практически не применяется.
В табл. 27 для приведенного примера сопоставлены результаты выбора альтернатив с помощью рассмотренных критериев. На первый взгляд кажется нелепым, что наилучшая альтернатива зависит от метода ее определения. На самом деле здесь нет противоречия, поскольку метод выбора учитывает индивидуальные предпочтения ЛПР.
Пример (продолжение)
Таблица 27. Сопоставление решений, полученных с использованием различных правил
| Р1 | Р2 | Р3 | Правило минимакса | Правило максимакса | Правило Грувича | Правило Сэвиджа | Правило Лапласа | |
| А1 | 92 | 160 | 40 | 40 | 160 | 76 | 100 | 96,3 |
| А2 | 100 | 76 | 120 | 76 | 120 | 89,2 | 84 | 98,7 |
| А3 | 68 | 80 | 140 | 68 | 140 | 89,6 | 80 | 96 |
| Ситуационнозависимые интерпретации | Принятие решений в условиях риска |