Нахождение решений в условиях определенности при множественности целей
В прескриптивной теории решений разработан целый ряд приемов для выбора альтернативы с учетом предпочтений ЛПР как в условиях определенности, так и в условиях риска, при одиночных и множественных целях.
Рассмотрим для примера нахождение решения в условиях определенности для случая множественных целей. Для этого требуется вначале определить мультиатрибутивную функцию ценности ЛПР. С помощью этой функции отражается (в интересах и по поручению ЛПР) его предпочтение относительно множества его целей, чтобы облегчить принятие решения.
Для простоты рассмотрим случай независимости атрибутов целей.
Предположим, что выпускник университета ищет место работы. Он определил, что основными параметрами (атрибутами) для него являются годовая зарплата и длительность рабочей недели. В результате поиска он получил три предложения (табл. 17).
Таблица 17
| Альтернативы | Годовая зарплата, $ | Длительность рабочей недели, ч |
| Консалтинговая фирма | 80000 | 60 |
| Университет | 50000 | 40 |
| Школа | 30000 | 20 |
Прескриптивная теория располагает рядом экспериментальных методов определения функции ценности ЛПР при одной цели, хотя это и не тривиальная задача. Она может быть сильно нелинейной в зависимости от индивидуального характера ЛПР (рис. 13).
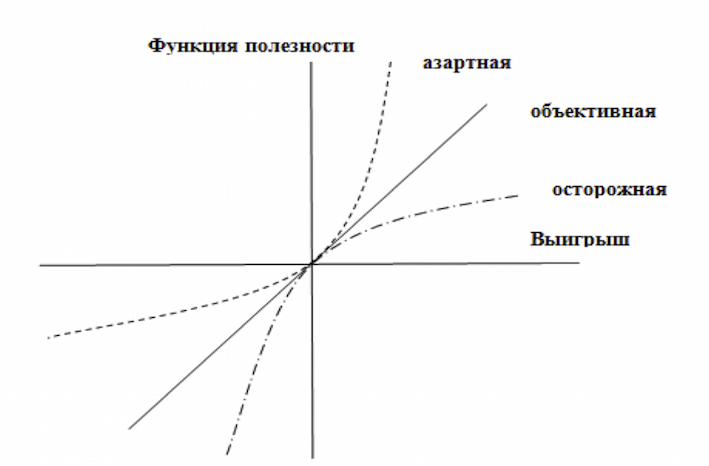
Рисунок 13. Функция полезности выигрыша
Допустим, мы определили функции полезности для нашего выпускника для обоих атрибутов цели – годовой зарплаты и длительности рабочей недели (рис. 14). Функции нормируются на интервал [0, 1], т.е. все релевантные значения параметров должны лежать между худшим значением, равным 0, и лучшим значением, равным 1. Границы (минимальное и максимальное значение параметра) могут быть взяты несколько шире, чем в рассматриваемых альтернативах, чтобы при появлении дополнительных альтернатив с несколько выходящими за первоначальные рамки значениями не было необходимости выполнять нормирование заново. Скажем, для рассматриваемого примера диапазон зарплаты можно взять от 25000 до 90000.
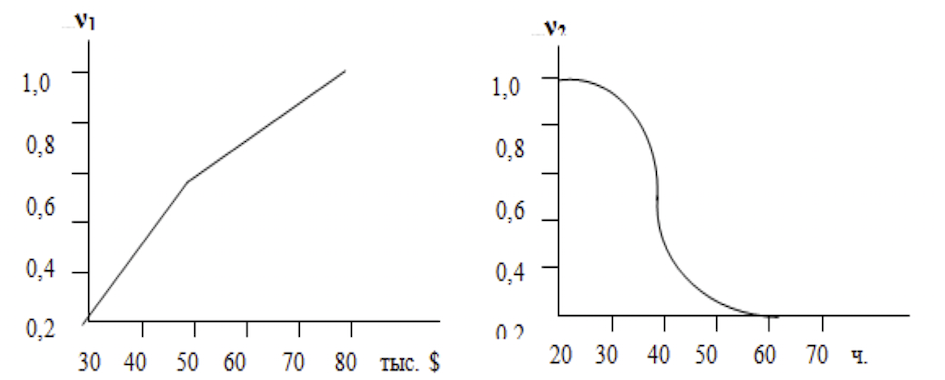
Рисунок 14. Функция полезности 
Далее необходимо учесть весовые коэффициенты атрибутов. Для этого также разработан целый ряд приемов. Предположим, что для условий нашего примера веса составляют 0,6 и 0,4 для зарплаты и продолжительности рабочей недели соответственно. Тогда можем составить таблицу (табл. 17).
Таблица 17
| Альтернативы | Ценность зарплаты | Взвешенная ценность зарплаты | Ценность продолжительности рабочей недели | Взвешенная ценность продолжительности рабочей недели | Суммарная ценность альтернативы |
| Консалтинговая фирма | 1,0 | 0,6 | 0,0 | 0,00 | 0,60 |
| Университет | 0,60 | 0,36 | 0,5 | 0,20 | 0,56 |
| Школа | 0,0 | 0,00 | 1,0 | 0,40 | 0,40 |
Из таблицы видно, что лучшей альтернативой является «Консалтинговая фирма». Такое простое решение возможно только в случае независимости предпочтений. В противном случае задача резко осложняется, хотя и для таких ситуаций в рамках прескриптивной теории имеются решения.
В целом для сложных и ответственных задач методы прескриптивной теории решений реально и успешно применяются. При этом всю техническую работу выполняют специалисты консалтинговых фирм или университетов. Окончательное решение, естественно, остается за ЛПР, которому представляются все расчеты и обоснования.
Широкому применению методов прескриптивной теории решений на практике препятствуют большие затраты времени на определение функций ценности и весов, сомнения в их стабильности для ЛПР, а также целый ряд дополнительных сложностей и возможных ошибок. Так, к примеру, имеется тенденция приписывать цели при декомпозиции ее на несколько подцелей больший суммарный вес, чем не разложенной цели. Для задач, связанных с принятием решений в условиях риска, большие сложности возникают с определением вероятности событий, хотя и для этих условий разработан целый набор приемов, помогающих уточнить субъективные оценки вероятностей событий.
Каждый метод и каждая модель прескриптивной теории решений требует от ЛПР однозначного согласия с условиями и ограничениями на их применение. Однако интуитивное поведение ЛПР, их интуитивные предпочтения могут существенно отличаться от описываемых теорией полезности. Хотя экспериментально подтверждено (например, В.В. Кочетковым и И.Г. Скотниковой), что индивидуально устойчивые особенности принятия решений, выступающие для конкретного человека как стилевые, могут быть реально выделены, проблем на этом пути много.
Для иллюстрации в следующем разделе приведено несколько известных парадоксов.
| Принятие решений в условиях определенности | Метод Парето решения многокритериальных задач выбора альтернативы |