Парадоксы интуитивных предпочтений
Статистике можно доверять только тогда, когда ее сам фальсифицировал.
У. Черчилль
«Эффект владения»
Предельная цена, по которой ЛПР еще готово было бы купить товар, и предельная цена, по которой ЛПР еще готово было бы продать товар, не должна бы, в принципе, отличаться. Однако при опросах ЛПР обнаруживается, что цена продажи, как правило, существенно выше цены, за которую лицо готово было бы купить товар. Это соотношение подвержено широким колебаниям, но в большинстве экспериментов превышало двойку.
Для наглядности сравним два вопроса:
- Сколько максимально вы были бы готовы заплатить, чтобы предотвратить возможность тяжелого заболевания с вероятностью 0,1%?
- Сколько вам нужно было бы заплатить, чтобы вы рискнули принять на себя возможность тяжелого заболевания с вероятностью 0,1%? Обычно соотношение сумм при ответах на эти вопросы превышает порядок.
Аналогичный пример: вам хочется пойти на концерт. Билет стоит 300 руб., но в кассе билетов нет. За какую максимальную сумму вы были бы готовы купить билет с рук? И наоборот, вы купили билет в кассе. За какую сумму вы были бы готовы его продать?
Парадокс М. Але (M. Alais)
Сравним две лотереи, представленные на рис. 16.
В соответствии с аксиомой независимости предпочтения ЛПР для обеих пар альтернатив (a, b) и (a’, b') должны бы совпадать. Большинство ЛПР в первой паре отдает предпочтение альтернативе а (как более надежной), а во второй паре альтернативе b' (оба выигрыша рискованны, и предпочтение отдается выигрышу с большей суммой).
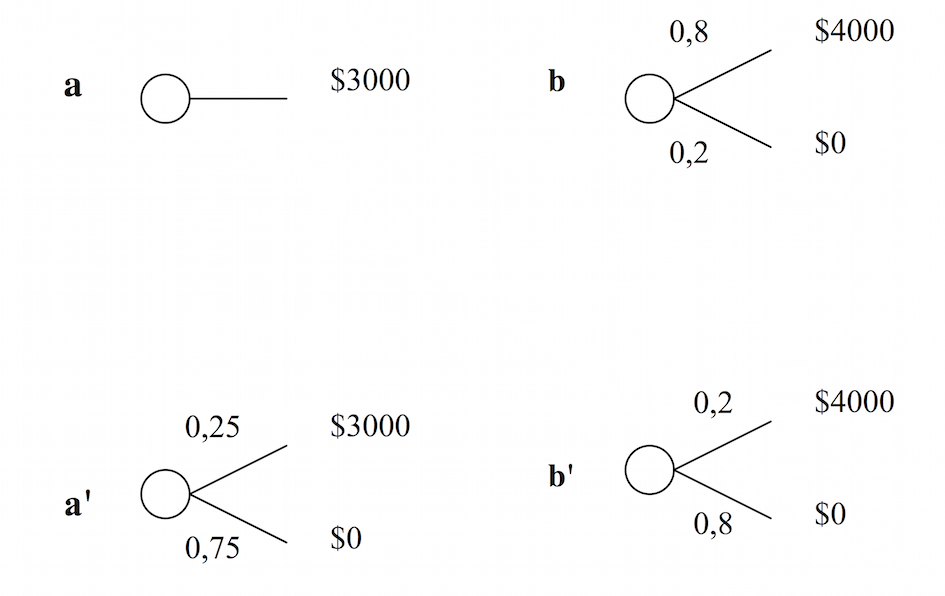
Рисунок 16. Парадокс М. Але
Парадокс Элсберга
Возьмем урну с 30 красными и 60 черными и желтыми шарами. Между черными и желтыми шарами возможно любое соотношение. Рассмотрим две пары альтернатив:
- а – выигрыш, если из урны вытаскивается красный шар;
- b – выигрыш, если из урны вытаскивается черный шар;
и
- a' – выигрыш, если вытаскивается один красный или желтый шар;
- b' – выигрыш, если вытаскивается один черный или желтый шар.
Большинство отдает предпочтение a по сравнению с b и b' по сравнению с a’, хотя в соответствии с аксиомой независимости предпочтений обе альтернативы идентичны. Вероятности выигрыша при выборе альтернативы a составляет 30/90, альтернативы b – от 1/90 до 59/90, альтернативы a’ – от 31/90 до 89/90, альтернативы b' – 60/90.
Искажение результатов при оценке вероятностей
Игральную кость с шестью гранями, четыре из которых красные ® и две зеленые (g), бросают 20 раз, и последовательность выпадения красной и зеленой граней фиксируется. Предлагаются три альтернативы:
- a: rgrrr;
- b: grgrrr;
- c: grrrrr.
Если одна из них выпадет в пределах всего сеанса, вы получаете выигрыш в $50.
В экспериментах 63 % выбрали серию b, 35 % выбрали серию a и 2 % выбрали серию c, хотя очевидно, что вероятность серии a максимальна.
Парадокс Симпсона
В 1972 году в Великобритании в округе Викхам (Whickham) было начато масштабное исследование влияния привычек на срок жизни (статья в журнале Clinical Endocrinology. 1977. No7 ). Из отобранных 1314 женщин были созданы две группы: женщины, которые курили (582 чел.), и женщины, которые до того никогда не курили (732 чел.).
Через 20 лет было установлено, что из курящих женщин в живых осталось 443 чел., т.е. 76 %, а из некурящих – 502 чел., т.е. 68 %.
| 582 курящих | 443 живы | 139 умерли | 76 % живых |
| 732 некурящих | 502 живы | 230 умерли | 68 % живых |
Какой вывод можно сделать из этого исследования? Курение продляет жизнь??
Дополнительная информация
Возрастная группа 18 – 44 года
| 288 курящих | 269 живы | 19 умерли | 93 % живых |
| 340 некурящих | 327 живы | 13 умерли | 96 % живых |
Возрастная группа 45 – 64 года
| 245 курящих | 167 живы | 78 умерли | 68 % живых |
| 199 некурящих | 147 живы | 52 умерли | 74 % живых |
Возрастная группа свыше 64 лет
| 49 курящих | 7 живы | 42 умерли | 14,3 % живых |
| 193 некурящих | 28 живы | 65 умерли | 14,5 % живых |
В младшей возрастной группе курили 46 %, в средней 55 %, а в старшей 20 %. Во всех трех возрастных группах шансы прожить следующие 20 лет у некурящих выше. Т.е. учет возраста в этом исследовании обязателен, иначе мы будем сравнивать пожилых некурящих с молодыми курящими.
«Проблема с козами» или Игра с условными вероятностями Проблема Монти Холла (Monty Hall)
Перед вами три закрытых двери. За одной из дверей автомобиль, который будет вам принадлежать, если вы в конце игры откроете именно эту дверь. За двумя другими дверями по козе. Вам нужно выбрать одну из дверей, но открыть ее сразу вы не имеете права.
Ведущий, который знает, за какой дверью находится автомобиль, открывает одну из дверей с козой и спрашивает, желаете ли вы остаться при своем выборе или хотите сменить дверь. Имеет ли смысл сменить дверь? Или это плохо? Анализ задачи (табл. 18) показывает, что имеет смысл сменить дверь: вероятность выигрыша в этом случае оказывается в два раза выше.
Таблица 18. Задача с козами
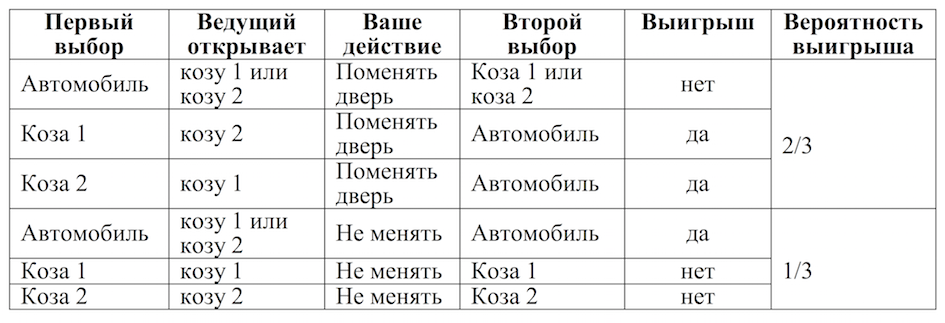
Феномен Ньюкомба-Бенфорда
Для ряда случайных чисел вероятность их появления одинакова. Однако в обычной жизни частота появления цифр нормального ряда от 1 до 9 подчиняется закону Ньюкомба-Бенфорда:
| Цифра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Частость, % | 30,1 | 17,6 | 12,5 | 9,7 | 7,9 | 6,7 | 5,8 | 5,1 | 4,6 |
Можно предложить следующую игру.
Если у участников игры сумма денег в кошелке начинается с цифр 4, 5, 6, 7, 8, 9, то ведущий платит им по 100 руб., если же сумма начинается с 1, 2 или 3, то они платят ведущему по 100 руб. При достаточно большом числе участников ведущий всегда выигрывает.
| Метод Парето решения многокритериальных задач выбора альтернативы | Ситуационнозависимые интерпретации |