Операции над множествами
Операции над множествами используются для образования новых множеств из данных множеств. Будем предполагать, что каждое из множеств, используемых в данном процессе, является подмножеством некоторого универсального множества, и будем требовать, чтобы вновь образованное множество было подмножеством того же самого универсального множества.
Обычно рассматриваются следующие операции над множествами:
- дополнение;
- объединение;
- пересечение;
- разность.
Для наглядного представления этих операций служат диаграммы Эйлера-Венна. Прямоугольник обозначает универсальное множество, а круги внутри него — подмножества.
Дополнением к множеству %%A%% называется множество элементов, которые не содержатся в %%A%%. Обозначается %%\overline{A}%%, читается «дополнение множества %%A%% к множеству %%U%%».
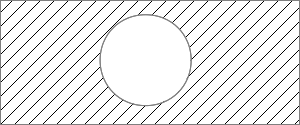
Дополнение множества
Пересечением множеств %%A%% и %%B%% называется множество элементов, которые принадлежат и %%A%%, и %%B%%. Обозначается %%A \cap B%%, читается «пересечение множеств %%A%% и %%B%%».
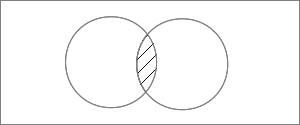
Пересечение множеств
Если %%A%% и %%B%% — непустые множества, пересечение которых пусто (%%A \cap B = \varnothing%%), то их называют непересекающимися множествами.
Объединением множеств %%A%% и %%B%% называется множество элементов, которые принадлежат либо %%A%%, либо %%B%% (либо обоим). Обозначается %%A \cup B%%, читается «объединение множеств %%A%% и %%B%%».
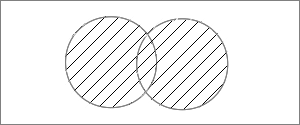
Объединение множеств
Разностью множеств %%A%% и %%B%% называется множество элементов, которые принадлежат %%A%% и не принадлежат %%B%%. Обозначается %%A \setminus B%%, читается «разность множеств %%A%% и %%B%%».
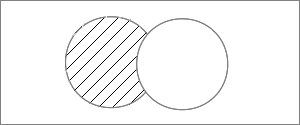
Разность множеств
| Сравнение множеств | Разбиения и покрытия |