Определение предела функции
Рассмотрим функцию %%f(x)%%, определенную, по крайней мере, в некоторой проколотой окрестности %%\stackrel{\circ}{\text{U}}(a)%% точки %%a \in \overline{\mathbb{R}}%% расширенной числовой прямой.
Понятие предела по Коши
Число %%A \in \mathbb{R}%% называют пределом функции %%f(x)%% в точке %%a \in \mathbb{R}%% (или при %%x%%, стремящемся к %%a \in \mathbb{R}%%), если, каково бы ни было положительное число %%\varepsilon%%, найдется положительное число %%\delta%%, такое, что для всех точек проколотой %%\delta%%-окрестности точки %%a%% значения функции принадлежат %%\varepsilon%%-окрестности точки %%A%%, или
$$ A = \lim\limits_{x \to a}{f(x)} \Leftrightarrow \forall\varepsilon > 0 ~\exists \delta > 0 \big(x \in \stackrel{\circ}{\text{U}}_\delta(a) \Rightarrow f(x) \in \text{U}_\varepsilon (A) \big) $$
Это определение называется определением на языке %%\varepsilon%% и %%\delta%%, предложено французским математиком Огюстеном Коши и используется с начала XIX века по настоящее время, поскольку обладает необходимой математической строгостью и точностью.
Комбинируя различные окрестности точки %%a%% вида %%\stackrel{\circ}{\text{U}}_\delta(a), \text{U}_\delta (\infty), \text{U}_\delta (-\infty), \text{U}_\delta (+\infty), \text{U}_\delta^+ (a), \text{U}_\delta^- (a)%% с окрестностями %%\text{U}_\varepsilon (A), \text{U}_\varepsilon (\infty), \text{U}_\varepsilon (+\infty), \text{U}_\varepsilon (-\infty)%%, получим 24 определения предела по Коши.
Геометрический смысл
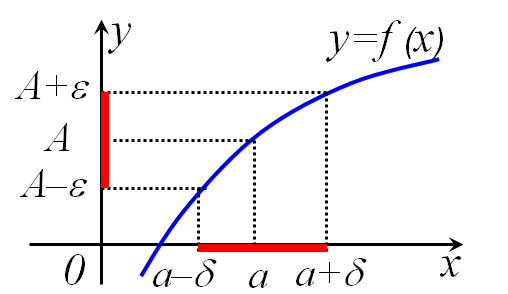
Геометрический смысл предела функции
Выясним, в чем заключается геометрический смысл предела функции в точке. Построим график функции %%y = f(x)%% и отметим на нем точки %%x = a%% и %%y = A%%.
Предел функции %%y = f(x)%% в точке %%x \to a%% существует и равен A, если для любой %%\varepsilon%%-окрестности точки %%A%% можно указать такую %%\delta%%-окрестность точки %%a%%, что для любого %%x%% из этой %%\delta%%-окрестности значение %%f(x)%% будет находиться в %%\varepsilon%%-окрестности точки %%A%%.
Отметим, что по определению предела функции по Коши для существования предела при %%x \to a%% не важно, какое значение принимает функция в самой точке %%a%%. Можно привести примеры, когда функция не определена при %%x = a%% или принимает значение, отличное от %%A%%. Тем не менее предел может быть равен %%A%%.
Определение предела по Гейне
Элемент %%A \in \overline{\mathbb{R}}%% называется пределом функции %%f(x)%% при %% x \to a, a \in \overline{\mathbb{R}}%%, если для любой последовательности %%\{x_n\} \to a%% из области определения, последовательность соответствующих значений %%\big\{f(x_n)\big\}%% стремится к %%A%%.
Определение предела по Гейне удобно использовать, когда возникают сомнения в существовании предела функции в данной точке. Если можно построить хотя бы одну последовательность %%\{x_n\}%% с пределом в точке %%a%% такую, что последовательность %%\big\{f(x_n)\big\}%% не имеет предела, то можно сделать вывод о том, что функция %%f(x)%% не имеет предела в этой точке. Если для двух различных последовательностей %%\{x'_n\}%% и %%\{x''_n\}%%, имеющих одинаковый предел %%a%%, последовательности %%\big\{f(x'_n)\big\}%% и %%\big\{f(x''_n)\big\}%% имеют различные пределы, то в этом случае также не существует предел функции %%f(x)%%.
Пример
Пусть %%f(x) = \sin(1/x)%%. Проверим, существует ли предел данной функции в точке %%a = 0%%.
Выберем сначала сходящуюся к этой точке последовательность $$ \{x_n\} = \left\{\frac{(-1)^n}{n\pi}\right\}. $$
Ясно, что %%x_n \ne 0~\forall~n \in \mathbb{N}%% и %%\lim {x_n} = 0%%. Тогда %%f(x_n) = \sin{\left((-1)^n n\pi\right)} \equiv 0%% и %%\lim\big\{f(x_n)\big\} = 0%%.
Затем возьмем сходящуюся к той же точке последовательность $$ x'_n = \left\{ \frac{2}{(4n + 1)\pi} \right\}, $$
для которой %%\lim{x'_n} = +0%%, %%f(x'_n) = \sin{\big((4n + 1)\pi/2\big)} \equiv 1%% и %%\lim\big\{f(x'_n)\big\} = 1%%. Аналогично для последовательности $$ x''_n = \left\{-\frac{2}{(4n + 1)\pi} \right\}, $$
также сходящейся к точке %%x = 0%%, %%\lim\big\{f(x''_n)\big\} = -1%%.
Все три последовательности дали разные результаты, что противоречит условию определения по Гейне, т.е. данная функция не имеет предела в точке %%x = 0%%.
Теорема
Определение предела по Коши и по Гейне эквивалентны.
| Предел функции | Односторонние пределы |