Задача управления запасами

Пример 1.1. Задача управления запасами. На складе хранится товар, которым обеспечивается сеть магазинов. Товар поступает на склад равными порциями через равные промежутки времени и расходуется с постоянной скоростью так, что к моменту очередного поступления его запасы становятся равными нулю (см. риc.).

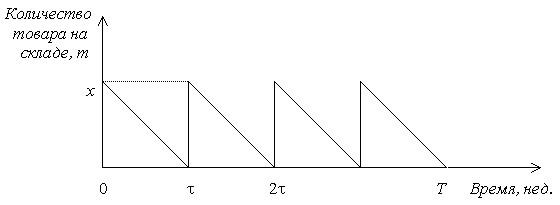
Рис. 1.1. Изменение запасов товара на складе во времени

Известны:

%%c_1%% — стоимость доставки одной порции товара (руб.),

%%c_2%% — стоимость хранения тонны товара в течение недели (руб./(т %%\times%% нед.)),

%%\tau%% — время между двумя последовательными поступлениями товара (нед.),

%%T%% — время обслуживания сети магазинов (плановый период, нед.),

%%N%% — необходимое количество товара в течение планового периода (спрос, %%т%%).

Требуется определить количество товара в порции так, чтобы общие затраты на обеспечение спроса %%N%% и хранение товара за время %%T%% были минимальными.

Перейдем к математической формулировке задачи. Обозначим через %%x%% искомое количество товара в порции (в тоннах). Подсчитаем отдельно затраты на доставку и хранение товара. На покрытие спроса %%N%% необходимо %%\frac{N}{x}%% доставок товара, затраты на которые (в руб.) составят

$$c_1 \frac{N}{x} ~~~~~~~~~~~~~(1.1)$$

За %%\tau%% недель (между двумя последовательными поставками) запасы товара на складе убывают с постоянной скоростью от %%x%% %%\tau%% до %%0%%, поэтому средний запас составит %%0.5x%% %%\tau%%.

Действительно, если бы товар не расходовался, то затраты на хранение за %%\tau%% недель равнялись бы %%c_2x τ%% руб., т.е. были пропорциональны площади %%x \tau%% прямоугольника со сторонами %%x%% и %%\tau%% (см. рис. 1.1). При равномерном расходовании товара затраты пропорциональны площади %%0.5x \tau%% прямоугольного треугольника с катетами %%x%% и %%τ%%, которая ровно в два раза меньше площади соответствующего прямоугольника. Следовательно, затраты (в руб.) на хранение товара в течение планового периода равны

$$c_2 (0.5x \tau)\left(\frac{N}{x}\right) ~~~~~~~~~~~ (1.2)$$

Складывая затраты (1.1) и (1.2), получим формулу общих затрат

$$\text{З}(x) = c_1\frac{N}{x} + c_2 (0.5xτ)\left(\frac{N}{x}\right)$$

Поскольку здесь %%\tau \left(\frac{N}{x}\right) = T%%, то окончательно получим

$$\text{З}(x) = c_1 \frac{N}{x} + 0.5 c_2 T x ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(1.3)$$

Итак, математически задача управления запасами заключается в нахождении такого положительного значения неизвестной %%x%%, при котором функция общих затрат (1.3) имеет минимум. В символической записи

$$ \text{З}(x) = c_1\frac{N}{x} + 0.5 c_2 T x \to \min~~~~~~~~~~~~~~~~~~~~(1.4)\\ x > 0 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(1.5) $$

Условие (1.4) задачи называют целевым, оно содержит требование (минимизации целевой функции), по которому находится искомое %%x%%. Условие (1.5), вытекающее из физического смысла неизвестной %%x%%, есть ограничение на %%x%%.

Задача управления запасами, содержащая ограничение на неизвестную %%x%%, относится к классу задач на условный экстремум. Конечно, здесь она предельно упрощена. Существуют более сложные постановки, которые учитывают нерегулярность поставок товара, ограниченную емкость склада и другие факторы. По образному выражению Г. Вагнера задача управления запасами “играет в исследовании операций такую же роль, как законы Ньютона в физике”.