Операции над событиями
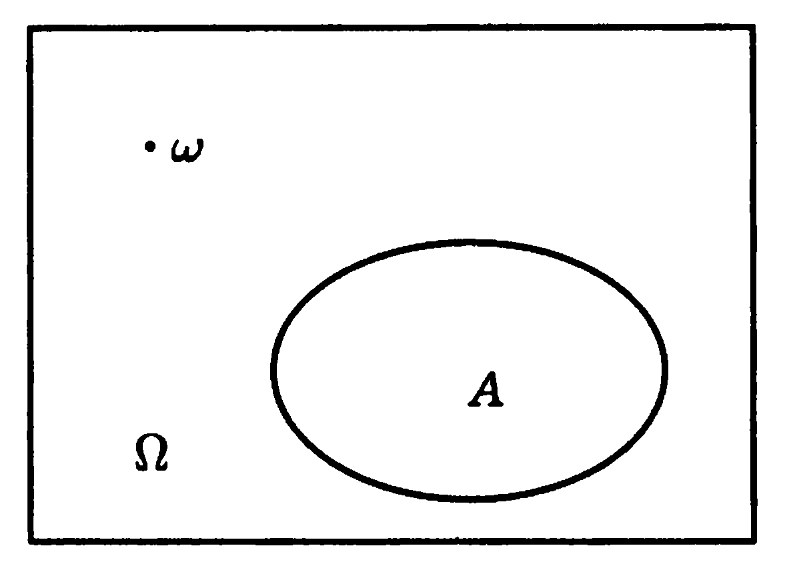
Рис. 1. Изображение диаграммы
Эйлера-Венна
Часто бывает полезно наглядно представить события в виде диаграммы Эйлера — Венна. Изобразим все пространство элементарных исходов прямоугольником (рис. 1). При этом, каждый элементарный исход %%\omega%% соответствует точке внутри прямоугольника, а каждое событие %%A%% — некоторому множеству точек, этого прямоугольника.
Рассмотрим теперь операции над событиями, которые совпадают с операциями над множествами.
Определение
Пересечением (произведением) двух событий %%A%% и %%B%% называют событие, обозначаемое %%A \cap B%% или %%AB%%, происходящее тогда и только тогда, когда одновременно происходят оба события %%A%% и %%B%%, т.е. событие, состоящее из тех и только тех элементарных исходов, которые принадлежат и событию %%A%%, и событию %%B%%.
События %%A%% и %%B%% называются несовместными, или непересекающимися, если их пересечение является невозможным событием, т.е. если %%A \cap B = \varnothing%%.
В противном случае события называют совместными, или пересекающимися.
Определение
Объединением (суммой) двух событий %%A%% и %%B%% называют событие, обозначаемое %%A \cup B%%, происходящее тогда и только тогда, когда происходит хотя бы одно из событий %%A%% или %%B%%, т.е. событие состоит из элементарных исходов, которые принадлежат хотя бы одному из множеств %%A%% или %%B%%.
Если события %%A%% и %%B%% несовместимы, то для обозначения могут использововать символ «%%+%%».
Например, поскольку невозможное событие %%\varnothing%% несовместно с любым событием %%A%%, то $$ \varnothing \cup A = \varnothing + A = A. $$
Аналогично определяют понятия произведения и суммы событий для любого конечного числа событий и даже для бесконечных последовательностей событий. Так, событие $$ A_1 A_2 \ldots A_n = \bigcap_{i = 1}^n A_i $$ состоит из элементарных исходов, принадлежащих всем событиям %%A_i, i = \overline{1,n}%%, а событие $$ A_1 \cup A_2 \cup \ldots \cup A_n = \bigcup_{i = 1}^n A_i $$ состоит из элементарных исходов, принадлежащих хотя бы одному из событий %%A_i, i = \overline{1,n}%%.
В частности, события %%A_1, A_2, \ldots, A_n%% называют попарно несовместными, если $$ A_i A_j = \varnothing $$ для любых %%i,j = \overline{1,n}, i \neq j%%, и несовместными в совокупности, если $$ A_1 A_2 \ldots A_n = \varnothing. $$
Определение
Разностью двух событий %%A%% и %%B%% называют событие, обозначаемое %% A \setminus B%%, происходящее тогда и только тогда, когда происходит событие %%A%% и не происходит событие %%B%%, т.е. состоит из тех элементарных исходов, которые принадлежат событию %%A%% и не принадлежат событию %%B%%
Определение
Дополнением события %%A%% называют новое событие, обозначаемое %%\overline{A}%%, происходящее тогда и только тогда, когда не происходит событие %%A%%. Так событие %%\overline{A}%% можно записать в виде: $$ \overline{A} = \Omega \setminus A. $$ Событие %%\overline{A}%% называют событием, противоположным событию %%A%%.
Определение
Событие %%A%% включено в событие %%B%%, если появление за собой события %%A%% обязательно влечет за собой наступление события %%B%%, или каждый элементарный исход события %%A%% принадлежит и событию %%B%%.
Приоритеты операций
Если некоторое событие записано в виде нескольких операций над различными событиями, то сначала выполняется операция дополнения, затем умножения, и, наконец, сложение и вычитание (слева направо).
Скобки могут увеличить приоритет любой из операций.
Пример
Рассмотрим устройство из %%n%% элементов. Элементы соединены последовательно, если устройство прекращает функционировать при отказе любого из элементов, и соединены параллельно, если прекращение функционирования наступает только при отказе %%n%% элементов (рис. 1а, 1б соответственно).
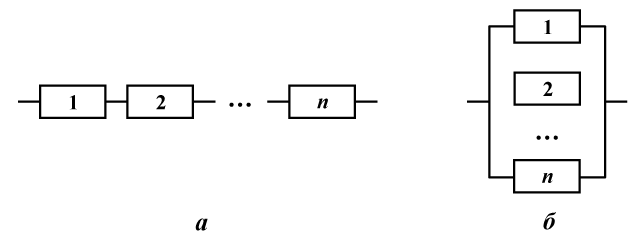
Рис 1. Последовательное и параллельное соединения
Обозначим %%A%% событие, означающее отказ системы, а %%A_i%% — отказ %%i%%-го элемента (%%i = \overline{1,n}%%). Тогда для последовательного соединения событие %%A%% представимо в виде: $$ A = A_1 \cup A_2 \cup \ldots A_n, $$ а для параллельного соединения $$ A = A_1 \cap A_2 \cap \ldots A_n. $$
Очевидно, что при параллельном соединении элементов событие %%A%% включено в каждое из событий %%A_i, i = \overline{1,n}%%, а при последовательном соединении любое событие %%A_i, i = \overline{1,n}%% включено в событие %%A%%.
| События | Свойства операций над событиями |