Основные понятия

Пусть $A, B, C, D, E, F$ — некоторые игроки в шахматы. Причем известно, что $A$ сыграл с $C, D, F$ (с последним два раза); $B$ сыграл с $C, E, F$; $C$ сыграл с $A, B$; D сыграл с $A, E, F$; $E$ сыграл с $B, D, F, E$; $F$ сыграл с $A$ (два раза) и с $B, D, E$. Информацию об этих играх можно проиллюстрировать следующей геометрической конфигурацией ($G$):

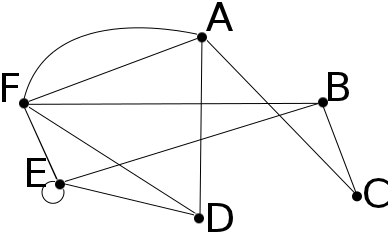
Построенная конфигурация полностью устанавливает информацию о встречах: игроки $X$ и $Y$ встречались, тогда и только тогда, когда в конфигурации $G$ соединены точки $X$ и $Y$ отрезком или дугой, причем количество таких дуг равно числу встреч игроков $X$ и $Y$. Если игрок $X$ сыграл сам с собой, то это будет тогда и только тогда, когда в конфигурации $G$ есть дуга, соединяющая точку $X$ с точкой $X$.

Конфигурация $G$ называется неориентированным графом (н-графом) или просто графом, при этом точки, изображающие $A, B, C, D, E, F$, называются вершинами графа $G$, а упомянутые дуги или отрезки, соединяющие вершины, называются ребрами графа $G$.

Заметим, что:

• в графе $G$ есть 2 ребра, соединяющие вершины $A$ и $F$. Такие ребра называются кратными или параллельными;
• ребра, соединяющие вершину с ней же, называются петлями;
• не исключено наличие вершин, не являющихся концом некоторого ребра (существование игрока, не сыгравшего ни одной партии).

Пусть $V = \{V_1, V_2,..., V_n\}$ — некоторое непустое множество произвольной природы элементов. $E$ — некоторое подмножество декартового произведения $V \times V \times N$, элементы которого называются ребрами. Тогда $G = (V, E)$ называется н-графом или графом, при этом элементы множества $V$ называются вершинами, а элементы множества $E$ ребрами данного графа.

Если $e = (V_i, V_j, k)$ — некоторое ребро графа $G$, то тройки $(V_i, V_j, k)$ и $(V_j, V_i, k)$ будем считать обозначением одного и того же ребра $e$.

Если вершины $V_i, V_j$ — концы ребра $e$, будем говорить, что вершины $V_i$, $V_j$ инцидентны ребру $e$ или ребро $e$ инцидентно вершинам $V_i$ и $V_j$. Два ребра, инцидентные одной вершине, называются смежными. Две вершины, инцидентные одному ребру, также называются смежными.

Вершина графа, не инцидентная ни одному ребру графа, называется изолированной.

Ребро вида $(V_i, V_i, k)$ называется петлей.

Если для ребра $e = (V_i, V_j, k_1)$ тройка $(V_i, V_j, k_2)$, $k_1 \ne k_2$ также является ребром графа, то ребро $e$ будем называть кратным.

Граф называется полным, если каждые две различные его вершины соединены одним и только одним ребром.