Преобразование сообщений

Вернемся к обсуждению информационных процессов, связанных с преобразованием одних сигналов в другие. Ясно, что технически это осуществимо. Ранее сигналы и их последовательности -сообщения - были названы нами «материальными оболочками для информации», и, естественно, возникает вопрос: при изменении «оболочки» что происходит с его содержимым, т.е. с информацией? Попробуем найти ответ на него.

Поскольку имеются два типа сообщений, между ними, очевидно, возможны четыре варианта преобразований:

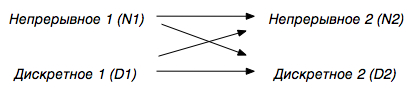
Осуществимы и применяются на практике все четыре вида преобразований. Рассмотрим примеры устройств и ситуаций, связанных с такими преобразованиями, и одновременно попробуем отследить, что при этом происходит с информацией.

Примерами устройств, в которых осуществляется преобразование типа %%N_1 → N_2%%, являются микрофон (звук преобразуется в электрические сигналы); магнитофон и видеомагнитофон (чередование областей намагничения ленты превращается в электрические сигналы, которые затем преобразуются в звук и изображение); телекамера (изображение и звук превращаются в электрические сигналы); радио-и телевизионный приемник (радиоволны преобразуются в электрические сигналы, а затем в звук и изображение); аналоговая вычислительная машина (одни электрические сигналы преобразуются в другие).

Особенностью данного варианта преобразования является то, что оно всегда сопровождается частичной потерей информации.

Потери связаны с помехами (шумами), которые порождает само информационное техническое устройство и которые воздействуют извне. Эти помехи примешиваются к основному сигналу и искажают его. Поскольку параметр сигнала может иметь любые значения (из некоторого интервала), то невозможно отделить ситуации: был ли сигнал искажен или он изначально имел такую величину. В ряде устройств искажение происходит в силу особенностей преобразования в них сообщения, например в черно-белом телевидении теряется цвет изображения; телефон пропускает звук в более узком частотном интервале, чем интервал человеческого голоса; кино- и видеоизображение оказываются плоскими, они утратили объемность.

Теперь обсудим общий подход к преобразованию типа %%N → D%%. С математической точки зрения перевод сигнала из аналоговой формы в дискретную означает замену описывающей его непрерывной функции времени %%Z(t)%% на некотором отрезке %%[t_1, t_2]%% конечным множеством (массивом) %%{Z_i, t_i}%% (i=%%0...n%%, где n - количество точек разбиения временного интервала).

Подобное преобразование называется дискретизацией непрерывного сигнала и осуществляется посредством двух операций: развертки по времени и квантования по величине сигнала.

Развертка по времени состоит в том, что наблюдение за значением величины %%Z%% производится не непрерывно, а лишь в определенные моменты времени с интервалом %%∆t%%: $$∆t=\frac{t_n-t_0}{n} $$

Квантование по величине - это отображение вещественных значений параметра сигнала в конечное множество чисел, кратных некоторой постоянной величине - шагу квантования (%%∆Z%%).

Совместное выполнение обеих операций эквивалентно нанесению масштабной сетки на график %%Z(t)%%, как показано на рис.1.2. Далее, в качестве пар значений %%{Z_i, t_i}%% выбираются узлы сетки, расположенные наиболее близко к %%Z(t_i)%%. Полученное таким образом множество узлов оказывается дискретным представлением исходной непрерывной функции. Таким образом, любое сообщение, связанное с ходом %%Z(t)%%, может быть преобразовано в дискретное, т.е. представлено посредством некоторого алфавита.

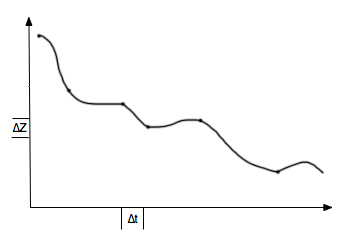
Рис.1-2. Дискретизация аналогового сигнала за счет операций развертки по времени и квантования по величине

При такой замене довольно очевидно, что чем меньше %%n%% (больше %%∆t%%), тем меньше число узлов, но и точность замены %%Z(t)%% значениями %%Z_i%% будет меньшей. Другими словами, при дискретизации может происходить потеря части информации, связанной с особенностями функции %%Z(t)%%. На первый взгляд кажется, что увеличением количества точек %%n%% можно улучшить соответствие между получаемым массивом и исходной функцией, однако полностью избежать потерь информации все равно не удастся, поскольку %%n%% - величина конечная.

Ответом на эти сомнения служит так называемая теорема отсчетов, доказанная в 1933 г. В. А. Котельниковым (по этой причине ее иногда называют его именем), значение которой для решения проблем передачи информации было осознано лишь в 1948 г. после работ К. Шеннона. Теорема, которую примем без доказательства, но результаты будем в дальнейшем использовать, гласит:

Непрерывный сигнал можно полностью отобразить и точно воссоздать по последовательности измерений или отсчетов величины этого сигнала через одинаковые интервалы времени, меньшие или равные половине периода максимальной частоты, имеющейся в сигнале.

Любое подобное устройство использует не весь спектр частот колебаний, а лишь какую-то его часть; например, в телефонных линиях используются колебания с частотами от 300 Гц до 3400 Гц. Согласно теореме отсчетов определяющим является значение верхней границы частоты - обозначим его %%v_m%%.

Смысл теоремы в том, что дискретизация не приведет к потере информации и по дискретным сигналам можно будет полностью восстановить исходный аналоговый сигнал, если развертка по времени выполнена в соответствии со следующим соотношением: $$∆t\leqslant\frac{1}{2v_m} $$

Можно перефразировать теорему отсчетов:

Развертка по времени может быть осуществлена без потери информации, связанной с особенностями непрерывного (аналогового) сигнала, если шаг развертки не будет превышать %%∆t%%, определяемый в соответствии с (1.1).

Например, для точной передачи речевого сигнала с частотой до %%v_m = 4000%% Гц при дискретной записи должно производиться не менее 8000 отсчетов в секунду; в телевизионном сигнале %%v_m = 4%% МГц, следовательно, для его точной передачи потребуется около 8000000 отсчетов в секунду.

Однако, помимо временной развертки, дискретизация имеет и другую составляющую - квантование.

Какими соображениями определяется шаг квантования %%∆Z%%? Любой получатель сообщения - человек или устройство - всегда имеют конечную предельную точность распознавания величины сигнала.

Например, человеческий глаз в состоянии различить около 16 миллионов цветовых оттенков; это означает, что при квантовании цвета нет смысла делать большее число градаций. При передаче речи достаточной оказывается гораздо меньшая точность - около 1%; следовательно, для амплитуды звуковых колебаний %%∆Z = 0,01\cdot Z^{max}%%, а алфавит для обозначения всех градаций громкости должен содержать 100 знаков. {.block.example}

Приходим к заключению, что шаг квантования определяется чувствительностью приемного устройства.

Указанные соображения по выбору шага развертки по времени и квантования по величине сигнала лежат в основе оцифровки звука и изображения. Примерами устройств, в которых происходят такие преобразования, являются сканер, модем, устройства для цифровой записи звука и изображения, лазерный проигрыватель, графопостроитель.

Термины «цифровая запись», «цифровой сигнал» следует понимать как дискретное представление с применением двоичного цифрового алфавита.

Таким образом, преобразование сигналов типа %%N → D%%, как и обратное %%D → N%%, может осуществляться без потери содержащейся в них информации.

Преобразование типа %%D_1 → D_2%% состоит в переходе при представлении сигналов от одного алфавита к другому - такая операция носит название перекодировка и может осуществляться без потерь.

Примерами ситуаций, в которых осуществляются подобные преобразования, могут быть: запись-считывание с компьютерных носителей информации; шифровка и дешифровка текста; вычисления на калькуляторе.

Таким образом, за исключением %%N_1 → N_2%% в остальных случаях оказывается возможным преобразование сообщений без потерь содержащейся в них информации. При этом на первый взгляд непрерывные и дискретные сообщения оказываются равноправными. Однако на самом деле это не так. Сохранение информации в преобразованиях %%N → D%% и %%D → N%% обеспечивается именно благодаря участию в них дискретного представления. Другими словами, преобразование сообщений без потерь информации возможно только в том случае, если хотя бы одно из них является дискретным. В этом проявляется несимметричность видов сообщений и преимущество дискретной формы. К другими ее достоинствам следует отнести:

• высокую помехоустойчивость;
• простоту и, как следствие, надежность и относительную дешевизну устройств по обработке информации;
• точность обработки информации, которая определяется количеством обрабатывающих элементов и не зависит от точности их изготовления;
• универсальность устройств.

Последнее качество - универсальность - оказывается следствием того обстоятельства, что любые дискретные сообщения, составленные в различных алфавитах, посредством обратимого кодирования можно привести к единому алфавиту. Это позволяет выделить некоторый алфавит в качестве базового (из соображений удобства, простоты, компактности или каких-либо иных) и представлять в нем любую дискретную информацию. Тогда устройство, работающее с информацией в базовом алфавите, оказывается универсальным в том отношении, что оно может быть использовано для переработки любой иной исходной дискретной информации. Таким базовым алфавитом, как увидим в дальнейшем, является двоичный алфавит, а использующим его универсальным устройством - компьютер.

Несимметричность непрерывной и дискретной информации имеет более глубокую основу, чем просто особенности представляющих сигналов. Дело в том, что информация, порождаемая и существующая в природе, связана с материальным миром - это размеры, форма, цвет и другие физические, химические и прочие характеристики и свойства объектов. Данная информация передается, как было сказано, посредством физических и иных взаимодействий и процессов. Бессмысленно ставить вопросы: для чего существует такая информация и кому она полезна? Эту природную информацию можно считать хаотической и неупорядоченной, поскольку никем и ничем не регулируется ее появление, существование, использование. Чаще всего она непрерывна по форме представления. Напротив, дискретная информация - это информация, прошедшая обработку - отбор, упорядочение, преобразование; она предназначена для дальнейшего применения человеком или техническим устройством.

Дискретная информация даже может не иметь прямого отношения к природе и материальным объектам, например представления и законы математики. Другими словами, дискретная - это уже частично осмысленная информация, т.е. имеющая для кого-то смысл и значение и, как следствие, более высокий (с точки зрения пользы) статус, нежели непрерывная, хаотичная. Однако в информатике, как было сказано, этот смысл не отслеживается, хотя и подразумевается. Эту же мысль можно выразить иначе: информатика имеет дело не с любой информацией и не с информацией вообще, а лишь с той, которая кому-то необходима; при этом не ставятся и не обсуждаются вопросы «Зачем она нужна?» и «Почему именно эта?» - это определяет потребитель информации.

Отсюда становится понятной приоритетность дискретной формы представления информации по отношению к непрерывной в решении глобальной задачи автоматизации обработки информации. Приведенные в данном параграфе соображения позволяют нам в дальнейшем исследовать только дискретную информацию, а для ее представления (фиксации) использовать некоторый алфавит. При этом нет необходимости рассматривать физические особенности передачи и представления, т.е. характер процессов и виды сигналов. Полученные результаты будут справедливы для любой дискретной информации независимо от реализации сообщения, с которым она связана. С этого момента и начинается наука информатика.